Транспортировка пучка. Оптика пучка в отсутствие коллективных эффектов. Теорема Буша и уравнение параксиального луча, страница 8

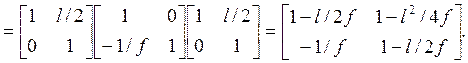C                            (38)

Как и у всех матриц преобразования, ее детерминант равен единице. Когда число линз и пролетных промежутков велико, анализ каждой индивидуальной траектории с помощью последовательности матриц преобразования может занимать много времени, хотя такой способ не представляет затруднений при численном моделировании. Если матрицы могут быть представлены последовательностью идентичных элементов, каждый из которых характеризуется матрицей преобразования А, то

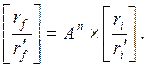                                                                                                                             (39)

Движение иона по траектории в такой системе устойчиво, только если модуль следа матрицы удовлетворяет соотношению

                                                                                                                                          (40)

В этом случае орбита иона является периодической с угловым опережением по фазе μ, определяемым формулой

  (41)

Если абсолютное значение Тr(А/2) превышает единицу, движение иона неустойчиво, и ион покидает периодический канал.

4.2. Транспортировка ламинарных пучков в собственных полях

В предыдущем разделе движение частиц пучка рассматривалось в предположении, что поля, создаваемые самим пучком, оказывают пренебрежимо малое влияние на траектории ионов. Такое описание оказывается адекватным при рассмотрении слаботочных пучков, но совершенно неправильно для сильноточных ионных пучков. Теперь мы попытаемся ответить на вопрос о величине собственных полей и их влиянии на пучок в предположении, что траектории ионов не пересекаются (т. е. течение ионов ламинарное) и ионный пучок является моноэнергетическим.

Пучок генерирует две разновидности поля: радиальное электрическое поле, обусловленное объемным зарядом пучка, и азимутальное магнитное поле, называемое током пучка. Если плотность объемного заряда — функция только r и θ , то электрическое поле описывается формулой

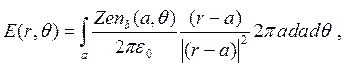                                                                            (42)

где r — радиус-вектор рассматриваемой точки; а — вектор, характеризующий положение элемента объема; А — поперечное сечение пучка.

Для однородного пучка уравнение (42) сводится к соотношению

                                                                                                         (43)

где r_о — радиус границы пучка.

Магнитная индукция может быть получена из закона Био-Савара и выражается формулой

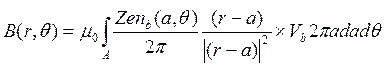 ,                                                                (44)

которая для однородного пучка принимает вид

                                                                                                     (45)

Сила, действующая на индивидуальный ион пучка, представляет собой силу Лоренца, которая выражается соотношением

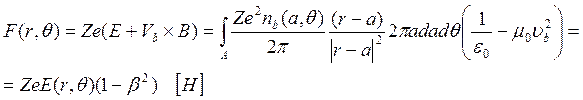                 (46)

Это соотношение имеет самый общий вид и применимо ко всем пучкам, подверженным действию поперечных сил. Оно также применимо для ускоренных пучков при условии, что j8 практически остается постоянным на расстоянии от оси, превышающем радиусу пучка.

4.2.1. Движение ионного пучка при отсутствии внешних полей

Движение иона под действием силы Лоренца определяется уравнением

,                                                                                                        (47)

где h — степень нейтрализации объемного заряда (рассматривается в разд. 4.3). Так как напряженность поля Е — линейная функция r для однородного пучка, траектории всех частиц идентичны, исключая фактор r/r_о. Следовательно, мы можем получить, без потери общности, внешнюю траекторию r_o(z) которая описывает огибающую ламинарного пучка из уравнения

Тогда

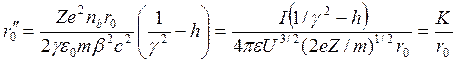                                                (48)

Здесь U и I— энергия и ток пучка; К— обобщенный первеанс пучка, который может быть выражен в виде

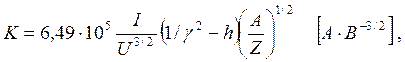                                                             (49)

где А — масса иона (а.е.м.).