Транспортировка пучка. Оптика пучка в отсутствие коллективных эффектов. Теорема Буша и уравнение параксиального луча, страница 19

                                                                                                                            (112)

Чтобы получить форму огибающей пучка, используем уравнения (106) и (ПО). Получаем уравнение

                                                                                                                  (113)

где  — нормализованный радиус огибающей пучка. Простым примером является однородно фокусирующий канал, в котором Р— постоянная величина. При таких обстоятельствах эллипс остается вертикальным и говорят, что пучок «согласован» с каналом. Величина

 в этом случае равна

                                                                                                                                                  (114)

Если пучок переносится из канала с силой  и пересогласовывается с каналом с силой  , то он обязательно проходит через область промежуточной фокусирующей силы , которая определяется формулой

                                                                                                                                                             (115)

Длина этой области должна быть такой, чтобы эллипс эмиттанса по-ворачивался на 90°.

4.4.5. Распределение Капчинского-Владимирского

Это распределение было впервые предложено Капчинским и Владимирским [34] и поэтому называется здесь К—В- раcпределением. Оно описывает однородно заполненную гиперэллипсоидальную трехмерную оболочку в четырехмерном фазовом пространстве х, x', у, у'. В согласованном однородно фокусирующем канале оси гиперэллипсоида параллельны координатным осям и распределение имеет вид

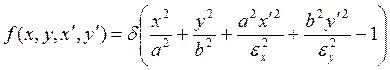                                                                                (116)

где  представляет -функцию. Это распределение имеет такое геометрическое свойство, что все его двумерные проекции однородны, так что плотность заряда в пучке — постоянная величина и собственные поля линейно зависят от радиуса. Если  , то поперечная энергия всех частиц одна и та же. Уолш [35] показал, что форм-фактор η используемый при определении яркости пучка, равен 2 в случае К— B-распределения.

К сожалению, К—В-распределение физически не вполне реалистично, поскольку в четырехмерном фазовом пространстве плотность пучка уменьшается по радиусу, т. е. пучок не является полым. Однако К-В-распределение обеспечивает удобную модель, которая может использоваться для анализа влияния собственного поля и дает результаты, находящиеся в хорошем соответствии с экспериментом. Уравнение (113) — уравнение огибающей пучка с дополнительным членом, связанным с эмиттансом пучка, но аксиальные поля из него исключены. Если пучок осесимметричен, то радиус огибающей пучка  заменяет   в уравнении (113) и в результате получается уравнение

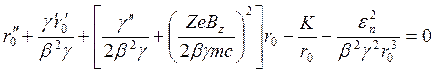                                                                    (117)

в котором влияние внешних полей учтено полностью и К— обобщенный первеанс.

Если  и  равны нулю, так что пучок согласован, и лишь собственные поля противодействуют расплыванию пучка, вызванному эмиттансом, то имеем соотношение

                                                                                                                                             (118)

при условии либо магнитного самостягивания, либо перенейтрализации ионного пучка. Если пучок не имеет осевой симметрии, Капчинский и Владимирский [34] показали, что для дрейфующих пучков уравнения огибающих записываются в виде

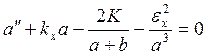                                                                                                                              (119)

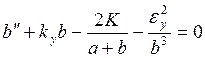                                                                                                                              (120)

где а и b— размеры огибающих в плоскостях х и у, k_x и k_у — внешние фокусирующие силы и K описывает влияние собственных полей. Аналогичные уравнения траекторий есть

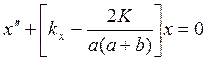                                                                                                                             (121)