Транспортировка пучка. Оптика пучка в отсутствие коллективных эффектов. Теорема Буша и уравнение параксиального луча, страница 12

                                                                                                                             (64)

где =_{обмен зарядом} + _{ионизация} ,n_b – плотность однородного пучка и - скорость пучка ионов, дает формулу

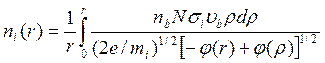                                                                                 (65)

в предположении, что ионная температура мала по сравнению с потенциалом φ (следовательно, ею можно пренебречь) и m_i — масса медленного иона. Единственное ограниченное решение для n_i(r) получается, когда справедливо разложение

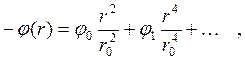                                                                                                     (66)

которое для малых r дает формулу

                                                                     (67)

Следовательно, n_i — постоянная величина (как и плотность пучка), пока членами более высокого порядка можно пренебрегать в разложении φ(r). Уравнение непрерывности для тепловых электронов легко полу-чить, приравнивая число производимых электронов к числу ушедших из пучка. Таким образом, можно написать

                                                                                                          (68)

Здесь  — сечение процесса ионизации и  — скорость электронов. Трак как электроны захватываются пучком благодаря пространственному потенциалу, они полностью термализуются и могут выйти из пучка, только набрав достаточную энергию. В этом случае плотность электронов определяется больцмановским распределением:

                                                                                                                 (69)

Здесь Т- электронная температура. Используя уравнение (66) и разлагая в ряд правую часть (69), получим

                                                                                                              (70)

Для вывода n_e0 предположим, что электроны движутся с тепловой скоростью за пределами пучка, где они практически не испытывают столкновений и могут выходить из пучка. Таким образом, когда

r = rо, подстановка выражения (69) в уравнение (68) дает формулу

                                                                     (71)

где φ — потенциал на границе пучка.

Уравнение энергетического баланса пучка может быть получено в предположении, что каждый электрон уносит энергию 2kT при выходе из плазмы [24]. Эта энергия является суммой кинетической энергии, которой он обладает в плазме, и приобретенной кинетической энергии, позволяющей ему выйти из плазмы. Если мы опишем процесс передачи энергии от ионов пучка к электронам простым сечением σ_u, то вклад объемной энергии в распределение электронов составит

                                                                                                                              (72)

Здесь U— энергия пучка в электронвольтах. Интегрирование по объему пучка дает

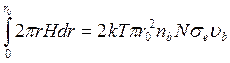                                                                                                         (73)

После интегрирования получаем

                                                                              (74)

Заключительной стадией анализа является использование условия электронейтральности для полного описания плазмы пучка. Это условие основывается на том обстоятельстве, что дебаевекая длина в плазме меньше, чем радиус пучка r₀. На оси, следовательно, справедливо соотношение

                                                                                                                                      (75)

где  — аксиальная плотность медленных ионов. Выполнив разложение, получаем

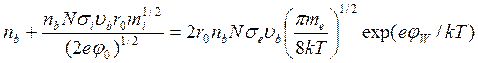
Это уравнение можно упростить, используя выражения (74):

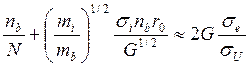                                                                                                    (76)

Здесь

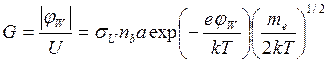                                                                                (77)

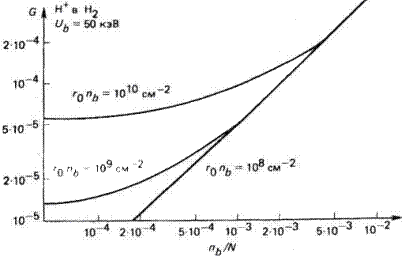
Рис. 4.10. Приведенный радиальный потенциал пучка G(= φ/U_b) как функция отношения плотности пучка к плотности газа.