Транспортировка пучка. Оптика пучка в отсутствие коллективных эффектов. Теорема Буша и уравнение параксиального луча, страница 15

Здесь m — масса отрицательного иона, а множитель (σ_е — σ_i)/σ_e обусловлен тем обстоятельством, что электроны, возникающие в процессе ионизации, не имеют направленной скорости, и считается, что они имеют нулевую скорость. Также пренебрегается передачей энергии пучка электронам. Покидающий пучок электрон уносит энергию 2кТ; поэтому уравнение энергетического баланса имеет вид

Если его скомбинировать с уравнением (82), то получим

                                                                                                                                                 (84)

Заключительный этап анализа — использование условия электронейтральности плазмы для вычисления относительного потенциала на границе пучка G, который дает разложение условия нейтральности на

                                                                                                                                       (85)

Следовательно,

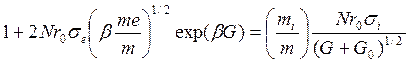                                                            (86)

Здесь G имеет такой же смысл, как и аналогичный член в случае положительных ионов, и равно отношению глубины потенциальной ямы к энергий пучка. На расстояниях, далеких от оси пучка, имеем

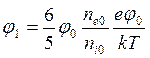                                                                                                                             (87)

Форма уравнения (86) сильно отличается от аналогичного выражения для пучка положительных ионов. Приведенный потенциал на границе пучка  не является функцией плотности n_b и зависит только от произведения N_ro. На рис. 4.15 представлена эта зависимость для пучка ионов Н с энергией 50 кэВ; можно видеть, что G растет от нуля при низких давлениях и достигает насыщения при высоких. Давление, соответствующее нулевому значению G, зависит от температуры медленных ионов (предположительно около 300 К). Этот положительный пространственный потенциал должен быть большим, чтобы обеспечивать достаточную фокусировку ионов пучка.

Нормализованные плотности чисел медленных ионов и электронов представлены на рис. 4.16 для случая, описанного выше. Эти ве-личины тоже не зависят от плотности пучка ионов, но с другой стороны проявляют зависимость, характерную для пучка положительных ионов, за исключением того, что роли электронов и ионов обращены.

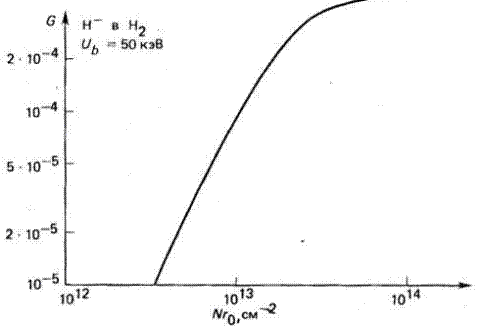
Рис. 4.15. Результаты расчета приведенного радиального потенциала как функции произведения плотности газа N на радиус пучка r₀ для пучка ионов Н^- в Н2.

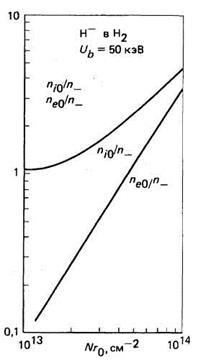
Рис. 4.16. Результаты расчета плотностей чисел медленных ионов и электронов, нормированных на плотность числа ионов Н^-, как функций плотности газа N и радиуса пучка r_о.

4.3.4. Влияние магнитных полей

Модели, описанные выше, основаны на предположении, что пучок однороден в осевом направлении, но такое предположение редко реализуется. В большинстве систем транспортировки пучков пучок обычно расплывается, а плотность газа изменяется на оси в результате сгущения или разрежения газа. К счастью, эти эффекты оказывают весьма умеренное влияние на степень нейтрализации пучка, потому что электроны в потенциальной яме пучка высоко подвижны в направлении оси пучка и удерживаются только благодаря заземлению пластины на ускорителе и взаимодействию с ионами пучка. В результате эта подвижность электронов оказывает усредняющее влияние на локальные изменения плотности газа, вследствие чего электронейтральность сохраняется даже в областях, где компенсация при иных обстоятельствах была бы слабой из-за низкой плотности газа. Наложение магнитного поля вызывает большое снижение подвижности электронов. Если поле перпендикулярно оси пучка, как в отклоняющем магните, то нижняя по потоку часть пучка полностью отделяется от его верхней части, и требуется отдельная подача газа для восстановления электронейтральности. Магнитные квадруполи в значительной степени оказывают такое же влияние. Быстрое изменение степени нейтрализации, вызываемое такими магнитами, усложняет задачу расчета огибающей пучка, и показывает, что для канала такого типа пучка нелегко выполнить условие нейтрализации объемного заряда.