Транспортировка пучка. Оптика пучка в отсутствие коллективных эффектов. Теорема Буша и уравнение параксиального луча, страница 4

Ускоряющие промежутки тоже можно описать, применяя матричный подход. Пирс [3] использовал матрицу вида

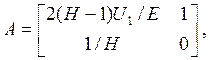                                                                                                              (16)

где  и - начальное и конечное значения кинетической энергии ионного пучка, Е — напряженность однородного аксиального электрического поля. Выражение (16) использовалось [4] для описания извлечения ионов из плазменного источника.

4.1.3. Фокусировка ионных пучков

Помимо коллимации пучка, осуществляемой ускоряющей системой ионного источника, часто необходимо иметь другие линзы вдоль канала транспортировки пучка, чтобы сохранять диаметр пучка приблизительно постоянным вдоль всего канала. В частности, это необходимо в ускорителях частиц, в которых аксиальная траектория иона может быть очень протяженной. Эти линзы могут быть как электростатическими, так и магнитными, и их свойства могут быть получены из решений уравнения (8) или (10).

Электростатические линзы. Вероятно, наиболее простой линзой является апертурная электростатическая линза, которая представляет собой тонкий диск с отверстием, через которое проходит пучок. Когда этот диск разделяет две области различающихся полей, как показано на рис. 4.2, генерируется радиальное электрическое поле, которое создает фокусирующую или дефокусирующую силу, линейно возрастающую по радиусу. Следовательно, линза может быть либо рассеивающей, либо собирающей в соответствии со знаком полей на каждой стороне. Фокусное расстояние может быть получено из уравнения (8), в котором член  полагается пренебрежимо малым по сравнению с другими. Получается соотношение

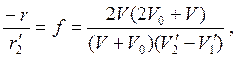                                                                                                       (17)

где и — напряженности электрических полей на выходной и входной сторонах линзы. Это выражение в нерелятивистском приближении сводится к формуле Дейвиссона и Калбрика [6]:

                                                                                                                             (18)

Сложностью следующего порядка в структуре электростатической линзы является устранение влияния дальнодействующих полей, существующих в линзе, представленной выше, путем помещения апертуры между двумя плоскостями, имеющими потенциал, равный объемному потенциалу пучка» так что она может использоваться в* канале транспортировки пучка без ускорения пучка. На рис. 4.3 показаны конструкции такой линзы, образованной системой труб или дисков с отверстием и обычно называемой одиночной линзой.

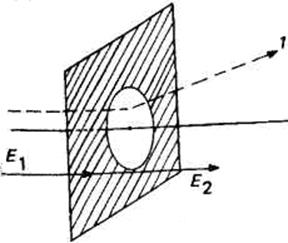
Рис. 4.2. Простая апертурная линза, у которой дефокусирующая сила  пропорциональна разности напряженностей электрических полей. 1 — траектория иона для рассеивающей линзы.

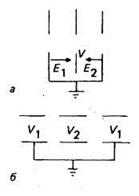
Рис. 4.3. Два типа одиночных линз, которые фокусируют пучок без изменения энергии пучка (в отличие от простой апертурной линзы), а — одиночная линза (всегда собирающая); б — цилиндрическая линза (всегда собирающая).

Пирс [3] показал, что простая одиночная линза, состоящая из трех тонких дисков, разделенных промежутками одинаковой длины L, при потенциале  на внешних дисках и  на внутреннем имеет фокусное расстояние , определяемое формулой

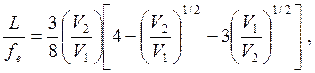                                                                                                  (19)

а главная плоскость находится на расстоянии от центра линзы, таком, что

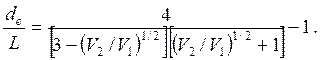                                                                                                 (20)

Зависимость от  показана на рис. 4.4; можно видеть, что данная линза при всех значениях , кроме 1, фокусирующая. Причина столь эффективной фокусировки в малой разнице между фокусирующей силой линз, находящихся на внешних дисках, относительно более сильной линзы, расположенной в центре. В результате эффективное фокусное расстояние оказывается большим по сравнению с размерами линзы. Это можно показать аналитически, если уравнение (19) разложить в ряд по параметру  Тогда безразмерная сила линзы  выразится соотношением