Транспортировка пучка. Оптика пучка в отсутствие коллективных эффектов. Теорема Буша и уравнение параксиального луча, страница 17

Очень часто плотность пучка неоднородна, и полезно ввести понятие «доля всех частиц пучка, которые расположены внутри площади, образованной контуром эмиттанса вдоль линии равной плотности». Иллюстрация такого определения дана на рис. 4.17. Интенсивно ис-

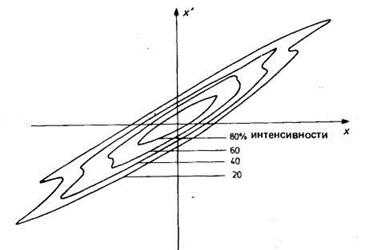
Рис. 4.17. Диаграммы поперечного эмиттанса, образованные контурами равной интенсивности. Такие диаграммы характеризуются квазитепловым распределением ионов по скоростям в направлении, ортогональном оси пучка.

следовался наиболее общий случай гауссова профиля пучка, обусловленного тепловым распределением ионов. В этом случае площадь эмиттанса пучка , содержащая долю всех ионов пучка, связана с  следующим образом:

                                                                                                                 (93)

Здесь ε_xсркв — среднеквадратичный эмиттанс, который был определен в работе [30] согласно соотношению

                                                                                                          (94)

где средние значения  и  включают весовые множители, определяемые интенсивностью пучка. Это определение отличается от первоначального тем, что величина  разделена на 4. Аналогичное выражение существует и для .

Одна из причин существования конечного эмиттанса заключается в ненулевой ионной температуре в ионном источнике» в котором ионы, образующие пучок, создаются путем ионизации. Среднеквадратичный эмиттанс можно непосредственно выразить через ионную температуру. Используем уравнение (94), при выводе которого предполагалось, что ионы выходят из плазмы параллельно оси пучка (несмотря на поперечное движение, обусловленное ионной температурой) со скоростью . Если ионы пучка выходят из источника через круглое отверстие радиусом а, то для однородного эмиттера

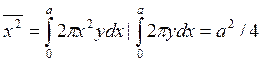                                                                                                 (95)

Для максвелловского распределения по скоростям, характеризуемого ионной температурой T_i, имеем

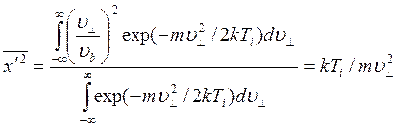                                                               (96)

Так как х и х' не связаны друг с другом, среднее значение их произведения равно нулю, что дает среднеквадратичный эмиттанс в виде

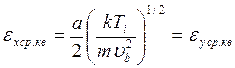                                                                                                                      (97)

Если энергия пучка не постоянна, то полезно ввести понятие «нормализованный эмиттанс пучка» согласно определению

                                                                                                                                               (98)

Таким образом,

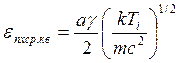                                                                                                                     (99)

Эмиттанс тесно связан с понятием «яркость пучка», которая определяется формулой

                                                                                                                   (100)

где η — величина порядка единицы (см. разд. 4.4.5). Более полезна нормализованная яркость, которая определяется как

                                                                                                            (101)

Если подставить выражение (97) в (101), чтобы исключить члены, содержащие эмиттанс, то получится соотношение

                                                                                                                                (102)

где j_i — плотность ионного тока в плоскости эмиссионного отверстия, непосредственно примыкающего к ионному источнику. Следовательно, яркость пучка в этом случае зависит лишь от параметров, определяемых ионным источником, и максимизируется при использовании источников, которые производят холодные ионы при высоких плотностях токов. Пучки ионов с большой массой имеют повышенную яркость, поскольку уменьшается поперечная скорость ио-нов при данной температуре.

4.4.3- Измерение эмиттанса пучка