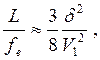 (21)
(21)
Где ![]() .
Величина
.
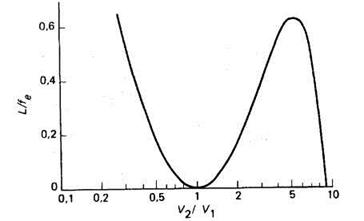
Величина ![]() больше нуля, т. е. линза фокусирующая. При
очень большом значении отношения
больше нуля, т. е. линза фокусирующая. При
очень большом значении отношения ![]() линза будет рассеивающей,
но ее использование не практично, поскольку энергия пучка на центральном диске
тогда во много раз превышает энергию инжекции. Более детальный анализ
реалистичных одиночных линз с различающимися диаметрами отверстий и конечной
толщиной электродов представлен в работе [7].
линза будет рассеивающей,
но ее использование не практично, поскольку энергия пучка на центральном диске
тогда во много раз превышает энергию инжекции. Более детальный анализ
реалистичных одиночных линз с различающимися диаметрами отверстий и конечной
толщиной электродов представлен в работе [7].
Магнитные линзы
Соленоид. Магнитным аналогом одиночной линзы является соленоид, который создает цилиндрически симметричные радиальное и аксиальное магнитные поля с помощью осесимметричных катушек. Фокусное расстояние может быть получено из уравнения (8), в котором V полагается равным нулю. Следовательно,
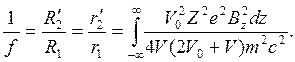 (22)
(22)
В нерелятивистском случае выражение для фокусного расстояния принимает вид
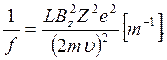 (23)
(23)
![]() Здесь В — магнитная индукция в единицах
тесла,
Здесь В — магнитная индукция в единицах
тесла, ![]() — импульс пучка, и считается, что поле
имеет трапецеидальную форму, так что аксиальная длина L — это расстояние между
точками половинной напряженности полей.
— импульс пучка, и считается, что поле
имеет трапецеидальную форму, так что аксиальная длина L — это расстояние между
точками половинной напряженности полей.
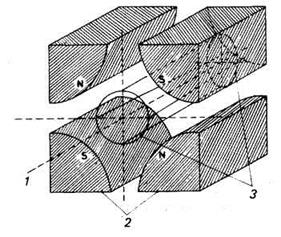
Рис. 4.5. Магнитная квадрупольная линза. Эта линза фокусирует в одной плоскости и дефокусирует в другой. 1 — ось пучка; 2 — магнитные полюса квадруполя; 3 — поперечное сечение пучка.
Как и в случае одиночной линзы, обратное фокусное расстояние пропорционально квадрату поля, т. е. соленоид — всегда фокусирующая линза. Фокусное расстояние пропорционально также энергии пучка, и именно это свойство делает соленоид неподходящим для высокоэнергичных пучков.
Квадруполь. Для высокоэнергичных (или высокомассовых) пучков более подходит квадрупольная линза, показанная на рис. 4.5. В этом случае движения в плоскостях х и у независимы, и поэтому нельзя использовать уравнения, приведенные в разд. 4.1.2, Теперь поле пропорционально поперечному смещению в ортогональном квадруполе, что дает
![]() (24)
(24)
Здесь а — расстояние от оси до поверхности полюса (рис. 4.5). Уравнения траектории могут быть получены непосредственно:
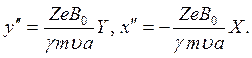
Решения имеют вид:
![]()
![]() (25)
(25)
Здесь ![]() — начальные положения и
углы,
— начальные положения и
углы, ![]() . Taким
образом, имеем следующие уравнения преобразования:
. Taким
образом, имеем следующие уравнения преобразования:
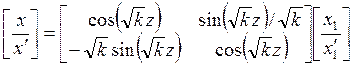 (26)
(26)
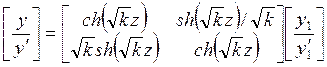
Детерминанты матриц преобразований равны единице. Аналогичное выражение существует для электростатических квадруполей при
![]() (27)
(27)
Квадрупольная линза фокусирует в одной плоскости и дефокусирует в другой и, следовательно, нарушает вращательную симметрию. Тем не менее ее фокусное расстояние много меньше, чем у соленоида, при одном и том же поле, и определяется формулой
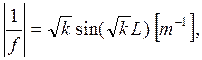 (28)
(28)
Где L - длина квадруполя. Фокусное расстояние — линейная функция магнитного поля и длины для коротких магнитовю.
Большинство квадруполей имеют конструкцию, показанную на рис.4.5 (если они магнитного типа), на котором поверхность полюсных наконечников имеет гиперболическую форму. Однако часто не-практично добиваться строго гиперболической формы поверхности полюсных наконечников, и вместо этого ее изготовляют в виде части цилиндрической поверхности. В работах [8, 9] были исследованы поля, создаваемые цилиндрическими полюсными наконечниками, и обнаружено, что для полностью симметричного магнита первую неквадрупольную составляющую поля дает 12-поль. Для полюсного наконечника, отделенного от противостоящего полюсного наконечника расстоянием 2a, наилучший радиус кривизны поверхности равен 1,15а, а угол сектора составляет 90°. Поле, создаваемое таким полюсным наконечником, является чисто квадрупольным при радиусах, меньших 0,9а. Таким образом, всегда имеет смысл минимизировать радиус пучка внутри магнита. Число ампер-витков, необходимых для создания магнитной индукции Во у полюсного наконечника, дается формулой
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.