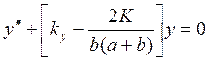Транспортировка пучка. Оптика пучка в отсутствие коллективных эффектов. Теорема Буша и уравнение параксиального луча, страница 20

                                                                                                                             (122)

4.4.6. Рост эмиттанса и нелинейная оптика

До сих пор рассматривались только линейные фокусирующие силы. Однако большинство полей линз или собственных полей содержат члены, в которых приложенное поле изменяется как третья или более высокая степень радиуса пучка. Эти аберрации нарушают форму эллипсов в фазовом пространстве, хотя и сохраняют первоначальную площадь эллипса. Но для цели транспортировки пучка важна площадь не исходного эллипса, а площадь нового эллипса, который заключает внутри себя искривленный эллипс фазового пространства и будет, конечно, больше по площади, чем исходный. Это соотношение иллюстрируется на рис. 4.22, где усиливающееся скручивание (искривление) исходного эллипса ведет к непрерывному возрастанию эффективного эмиттанса пучка вдоль оси пучка.

Эта проблема приобретает особую важность в периодически фокусирующих каналах, где искривление может развиваться, вызывая весьма значительный рост эмиттанса. Проблема обостряется тем, что пучки стремятся приобрести неоднородные радиальные профили, которые формируются вследствие нелинейности поля объемного заряда, хотя поля линзы являются линейными, что приводит к рассогласованию между полями линзы и объемного заряда. Это рассогласование рассмотрел Хофман [36], который показал, что рост эмиттанса пропорционален току пучка в канале и рассогласованию между идеальным однородным профилем и наблюдаемым профилем пучка. Измерения, выполненные Клабунде и др. [37], подтвердили эти теоретические модели.

Рис. 4.22. Рост эффективного эмиттанса, вызванный прохождением через систему линз. Действительный эмиттанс, однако, не изменяется. Штриховая линия ограничивает эффективную площадь в фазовом пространстве, сплошная линия — искаженную площадь.

4.5. Огибающая дрейфующего пучка

В предыдущих разделах мы рассматривали эволюцию уравнения параксиального луча от простого уравнения траектории иона к форме, Учитывающей вклад собственных полей и эмиттанса пучка. В настоящем разделе мы учтем эффекты нейтрализации объемного заряда пучка и получим уравнение огибающей дрейфующего пучка, решение которого имеет значение для большинства типов ионных источников, в частности инжекторов нейтральных пучков, используемых в термоядерных установках. Основные предположения состоят в том, что направляющее осевое магнитное поле отсутствует и канонический момент импульса равен нулю, что приводит уравнение (117) к виду

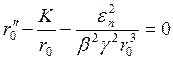                                                                                                                                      (123)

где члены с  и  также равны нулю из-за отсутствия ускоряющих электрических полей.

Величина К— обобщенный первеанс пучка [уравнение (48)], который может быть выражен через плотность пучка:

                                                                                                  (124)

Однако в разд. 4.3.2 и 4.3.3 влияние компенсации объемного заряда было учтено в форме  , где  — пространственный потенциал на границе пучка. Первеанс и пространственный потенциал можно взаимосогласовать с помощью определения величины h согласно формуле

                                                                                                                                                  (125)

где  Следовательно,

                                                                                                                                   (126)

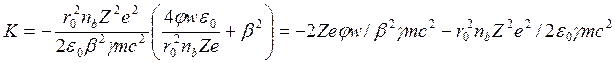                        (127)

Следует отметить, что  — отрицательная величина для пучков как положительных, так и отрицательных ионов; следовательно, К— положительная, но малая величина для пучка положительных ионов, за исключением случая релятивистских скоростей, и всегда отрицательная величина для отрицательных ионов пучка. В нерелятивистском пределе выражение для К принимает вид

                                                                                                                                   (128)