Транспортировка пучка. Оптика пучка в отсутствие коллективных эффектов. Теорема Буша и уравнение параксиального луча, страница 2

Следовательно, форма траектории ионов может быть выведена из уравнений движения, которые представлены здесь в релятивистском виде. Наиболее общая форма уравнения движения в ионной оптике известна как уравнение параксиального луча. Пучок имеет определенную ось, относительно которой определяется движение ионов, и приложенные силы представляются в виде разложения первого порядка относительно магнитной индукции на оси пучка. Основным предположением при выводе уравнения является малость угла между траекторией иона и осью пучка, что является хорошим приближением практически для любого реального пучка, даже если его ось искривлена (например, при ускорении энергичной частицы).

Поскольку большинство пучков в большой степени обладает цилиндрической симметрией, мы будем основывать все последующие выводы на этом предположении и получим уравнение параксиального луча в цилиндрических координатах. Вид уравнения в двумерной декартовой системе координат аналогичен. В последующем анализе всегда используется система единиц СИ.

4.1.1. Теорема Буша и уравнение параксиального луча

Буш [1] вывел выражение, описывающее движение частицы в акcиальносимметричном магнитном поле и связывающее угловую скорость частицы с магнитным потоком, пронизывающим траекторию частицы. Ситуация показана на рис. 4.1.

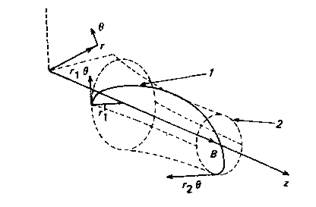
Рис. 4.1. Траектория движения заряженной частицы в аксиально-симметричном магнитном поле (к формулировке теоремы Буша). 1-траектория частицы; 2-граница площади, относительно которой рассматривается магнитный поток.

Сила Лоренца, действующая на ион, может быть приравнена скорости изменения момента импульса в соответствии со вторым законом Ньютона. Следовательно,

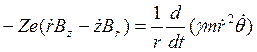                                                                    (1)

, где Z — зарядовое число, γ = (1-υ²/с²)^-1/2, m — масса покоя иона, точка над символом означает дифференцирование по времени. Составляющие индукции магнитного поля В_r и B_z относятся к случаю аксиальной симметрии. Движение в аксиальном и радиальном направлениях приводит к изменению магнитного потока Ф, пронизывающего траекторию частицы в поле. Это изменение Δ Ф выражается в виде

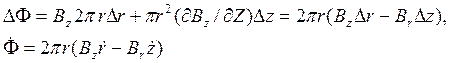                    (2)