Транспортировка пучка. Оптика пучка в отсутствие коллективных эффектов. Теорема Буша и уравнение параксиального луча, страница 21

4.5.1. Решение уравнения Капчинского — Владимирского

В разд. 4.4 было показано, что  является функцией N, n_b и r_о для данныx типа ионов и энергии пучка. Не существует простого выражения для  подстановка которого в уравнения (123) и (128) дала бы возможность получить общее аналитическое решение. Однако легко получить численные решения, которые показывают, что огибающая пучка положительных ионов близка к гиперболе. Тем не менее полезно попытаться найти аналитическое решение, чтобы получить представление о масштабе расплывания пучка при измерении основных параметров пучка. С помощью уравнений (123) и (128) можно получить соотношение

                                                                                                                      (129)

где . Если ток пучка сохраняется, то

                                                                                                                                                 (130)

Пространственный потенциал нейтрализованного пучка положительных  ионов может быть получен из уравнения (76) и равен

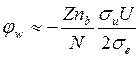                                                                                                                                              (131)

Объединение уравнений (129)—(131) дает соотношение

                                                                                                                                    (132)

где 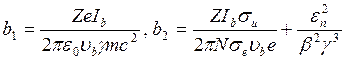 . В нерелятивистском пределе член  становится малым и решение уравнения (132) приближается к гиперболе с уравнением огибающей вида

                                                                                                                                          (133)

где А — радиус огибающей в самой узкой части пучка и  равно нулю.

Параметры самой узкой части пучка могут быть выражены через начальный радиус огибающей, угол сходимости пучка  и его производную .

                                                                                                                            (134)

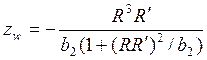                                                                                                                             (135)

Здесь — аксиальная координата сужения, отсчитанная от начального положения. Радиус пучка на мишени выражается формулой

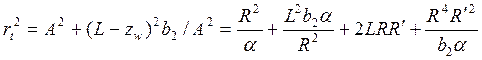
где — расстояние до мишени и  Следовательно,

                                                                                                       (136)

Величина минимальна при  , так что

                                                                                                                                                 (137)

Возвращаясь к уравнению (132), мы можем выразить  в форме

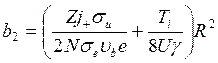                                                                                                                           (138)

Где  —начальная плотность тока пучка. Следовательно,

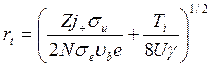
Холмс [22] исследовал этот эффект для фиксированных значений L и j+, увеличивая R так, что эффективный угол расходимости пучка , который определяется как  , уменьшался до очень малого значения, тогда как суммарный ток пучка нарастал как R². Его результаты представлены на рис. 4.23. При высоких энергиях пучка член, содержащий объемный заряд, в конечном счете доминирует.

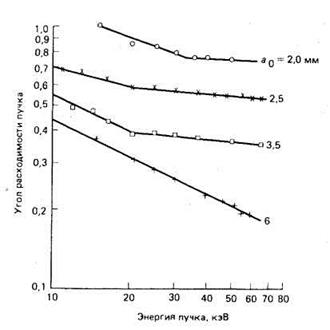
Рис. 4.23. Уменьшение угла расходимости, достигаемое путем увеличения радиуса пучка (при использовании больших извлекающих отверстий) при постоянной плотности первеанса пучка для Не+-пучка в Не [22].

В случае пучков отрицательных ионов, аналитический вид огибающей пучка получить трудно, так как влияния объемного заряда и эмиттанса взаимно противоположны. При высоких давлениях газа потенциал объемного заряда перестает зависеть от давления и тока пучка. Следовательно, можно ожидать, что огибающая приобретает форму осциллирующей кривой, так как член, связанный с эмиттансом, обратно пропорционален кубу радиуса пучка, тогда как член, связанный с объемным зарядом, обратно пропорционален только радиусу пучка, Величина этих осцилляции существенно зависит от начальных условий.