Величина G- отношение глубины потенциальной ямы к энергии
пучкa в электронвольтах. Для простоты предполагалось, что в формуле (74) ![]() много больше единицы.
много больше единицы.
Условие электронейтральности плазмы также выполняется вдали от оси пучка, где
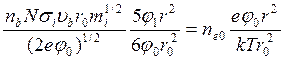
Следовательно,
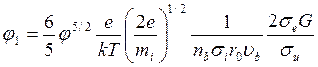
уравнения (76)—(78) полностью описывают плазму пучка посредством основных параметров пучка nb,r0,U и N, а также сечений соответствующих процессов. На рис. 4.10 показана зависимость величины G от отношения nb/N для нескольких значений nbr0 водородного Н + -пучка с энергией 50 кэВ. Можно видеть, что G линейно уменьшается с уменьшением nb/N от предельного значения 29IAl/2/U3/2 [где I— ток пучка (мА), А — масса иона (а.е.м.), U — энергия пучка (кэВ)] при низких значениях N, когда пучок полностью нескомпенсирован. При высоких плотностях газа G стремится к постоянному значению, которое увеличивается с ростом произведения nbr0. Такая зависимость наблюдалась экспериментально [22], и φw, измеренное эмитирующим ленгмюровским зондом, представлено как
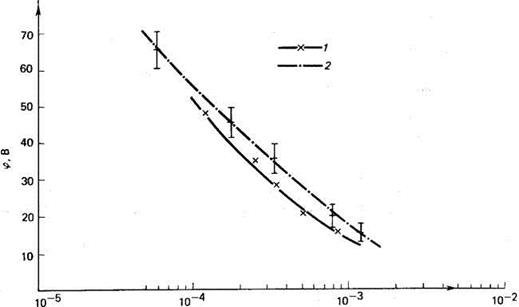
Рис. 4.11. Измеренный радиальный потенциал (φ) Не + -пучка с энергией 20 кэВ в Не в зависимости от давления газа р [22]. 1 — ленгмюровский зонд; 2 — энергетический зонд.
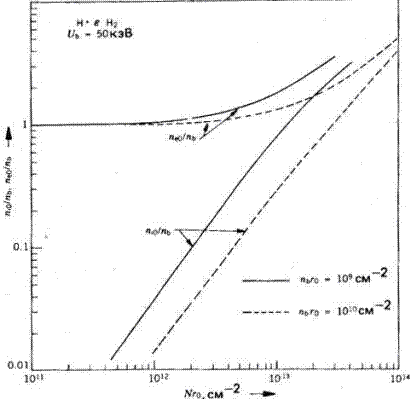
Рис. 4.12. Результаты теоретического расчета приведенных плотностей медленных ионов и электронов как функций произведения плотности газа N на радиус пучка rо.
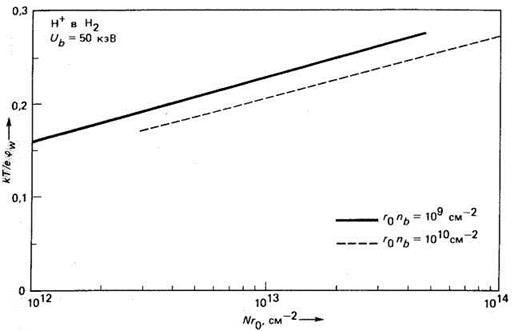
Рис. 4.13. Результаты теоретического расчета зависимости приведенной (относительно радиального потенциала пучка) электронной температуры от произведения плотности газа N на радиус пучка r0.
функция N на рис.4.11. для пучка с током 20 мА и энергией 20 кэВ. Со-вcем недавно такая зависимость φW от N была подтверждена использованием 200-кэВ А + -пучка и измерением φW по энергии медленных ионов, выходящих из пучка.
Насыщение глубины потенциальной ямы G достигается, когда плотность пучка ионов становится малой относительно rbо и nео. Это четко видно на рис. 4.12, где приведены зависимости парциальных плотностей пучка niо/nb и пео/nb от Nro для двух значений nbrо в случае протонного пучка с энергией 50 кэВ. При высоких плотностях газа пу-чок оказывается только источником частиц и пространственный потенциал принимает такое значение, при котором электроны и ионы имеют одинаковые плотности. При низких плотностях газа плотность числа медленных ионов пренебрежимо мала, хотя и нарастает приблизительно как N2r20, тогда как плотность числа электронов фактически равна плотности числа ионов пучка.
Зависимости приведенной электронной температуры кТ/еφW от Nrо показаны на рис. 4.13, Она медленно нарастает при увеличении давления, тогда как φW уменьшается и достигает насыщения. Следовательно, кТ имеет U-образную зависимость от Nr0 и практически не зависит от плотности пучка. Холмс [22] наблюдал эту зависимость экспериментально (рис. 4.14). Электронная температура измерялась по энергетическому распределению эмитированных электронов, полученному с использованием энерго-анализирующего зонда.
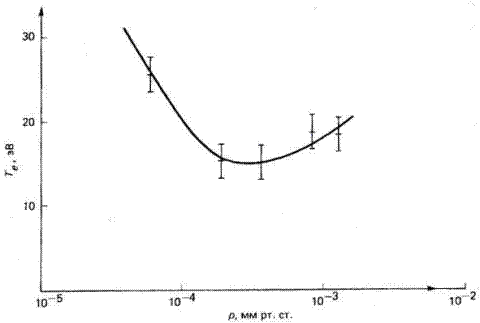
Рис. 4.14. Результаты измерения электронной температуры Те Не+ -пучка с энергией 20 кэВ в Не как функции давления гелия р [22].
4.3.3. Нейтрализация пучков отрицательных ионов
Естественно полагать, что нейтрализация пучков отрицательных ионов может уменьшить эффективный объемный заряд пучка на несколько процентов по сравнению с величиной для исходного пучка. Однако было обнаружено [25, 26], что пучок проявляет ион-ионную неустойчивость при давлениях ниже критического значения, когда наблюдается, что пучок имеет отрицательный плазменный потенциал, соответствующий суммарной отрицательной плотности объемного заряда. При более высоких давлениях пучок становится устойчивым и имеет положительный плазменный потенциал, который соответствует суммарной положительной плотности пространственного заряда.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.