Транспортировка пучка. Оптика пучка в отсутствие коллективных эффектов. Теорема Буша и уравнение параксиального луча, страница 16

Продольное поле, такое, как создаваемое в потоке Бриллюэна или в соленоидальном магните, допускает аксиальное движение электронов, и нейтрализация объемного заряда существенно не изменяется. Это поле уменьшало бы поперечную диффузию электронов без торможения медленных ионов; следовательно, пространственный потенциал уменьшился бы при приложении аксиального магнитного поля, что снизило бы расплывание объемного заряда.

4.4. НЕЛАМИНАРНЫЕ ПУЧКИ

4.4.1. Теорема Лиувилля

До сих пор мы рассматривали ламинарное течение ионов, так что в принципе пучки могли быть транспортированы в точку фокуса. К сожалению, реальные пучки не столь просты, и в любой точке пространства будет существовать пучок траекторий, наклоненных относительно главной оси, приводящий к неламинарному потоку. Мы рассмотрим такое поведение, используя понятие «фазовое пространство», в котором главные оси х, у, р_х и р_у используются для описания поперечного движения, z и p_z — аксиального; p_x,y,z — импульсы ионов в каждом из соответствующих направлений.

Движение в фазовом пространстве подчиняется теореме Лиувилля, которую мы изложим ниже в качестве первого этапа в понимании неламинарной транспортировки пучка. Эта теорема доказывается здесь с помощью методов Гамильтона, но Голдстейн [29] описывает более общий метод. Мы начнем с записи лагранжиана L для ансамбля частиц, находящегося под действием внешних потенциалов ¥и А, вызываемых электростатическим и магнитным полями;

                                                                                                         (88)

Лагранжиан не учитывает эффекты, вызываемые неконсервативными силами, например, приводящими к рассеянию. Канонический импульс определяется как

где x_i — положение i-й частицы. Гамильтониан определяется выражением

                                                                                                                                 (89)

Следовательно,

                                                                  (90)

Приведенные уравнения называются каноническими уравнениями Гамильтона, и для каждой степени свободы, т. е. для каждой оси фазового пространства пучка существует система таких уравнений. Во многих случаях, когда силы по каждой степени свободы независимы, можно существенно упростить понятие «фазовое пространство», но для импульса мы сохраним полноту описания.

Теорема Лиувилля основана на таком понимании фазового пространства и утверждает, что плотность числа невзаимодействующих частиц в шестимерном фазовом пространстве, находящихся под действием консервативных сил, инвариантна вдоль траектории частицы. Доказательство этой теоремы выполняется непосредственно: функция плотности  удовлетворяет уравнению непрерывности

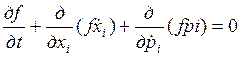,                                                                                                      (91)

в котором предполагается суммирование по индексу i от 1 до 3. Полная запись производных и подстановка выражения

дают

или                                                                                                                                      (92)

вдоль траектории частицы. Уравнение (92) выражает теорему Лиувилля. Таким образом, рассматриваемая система частиц (пучок) ведет себя как газ, т. е. занятая ею область фазового пространства может изменять свою форму, но не объем.

4.4.2. Эмиттанс и яркость

Для большинства ионных пучков, в которых векторный потенциал равен нулю (при пренебрежении собственным полем пучка), мы можем рассматривать движение в поперечной плоскости как не зависящее от аксиального движения пучка и разделенное с ним. Если траектории ионов к тому же близки к параксиальным, так что  и то сохранение объема фазового пространства сводится к сохранению площадей А(х, х') и А(у, у') в двух поперечных плоскостях фазового пространства. Каждая из этих площадей, деленная на π, называется эмиттансом пучка. Понятие «эмиттанс пучка» в направлении z не имеет смысла до тех пор, пока пучок не модулирован по времени, как в радиочастотных ускорителях, и не обсуждается здесь.