Таким образом,
энтропия жидкости при температуре плавления больше энтропии твердого тела;
энтропия γ-железа при температуре превращения больше, чем α-железа, белого
олова больше, чем серого. Мы знаем также, что энтропия раствора больше, чем
суммарная энтропия компонентов. Заметим, что формула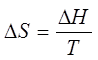 
справедлива
только для обратимых процессов, т.е. таких, которые с равной вероятностью идут
в прямом и обратном направлении. Таковы, например, процессы плавления или
кристаллизации при температуре плавления, когда твердая и жидкая фазы находятся
в равновесии. Стоит, однако, повысить или понизить температуру, как процесс
станет необратимым, т. е. будет идти только в одном направлении: тело будет
либо плавиться (Т>Тпл), либо кристаллизоваться (Т<Тпл).
Для необратимых процессов формула (202) приобретает вид 
,
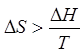поэтому, пользуясь ей, нельзя рассчитать величину ΔS,
а можно определить только ее нижний предел.
Как понять причины изменения энтропии? Согласно Больцману,
,
(206)
где k – постоянная Больцмана, равная 1,38.10-23 дж/град (1,38.10-16 эрг/град),
W – термодинамическая вероятность состояния системы или число способов, которым осуществляется данное макроскопическое состояние.
Следовательно, возрастание, энтропии означает переход системы от менее вероятных состояний к более вероятным, т. е. таким, которые осуществляются большим числом способов.
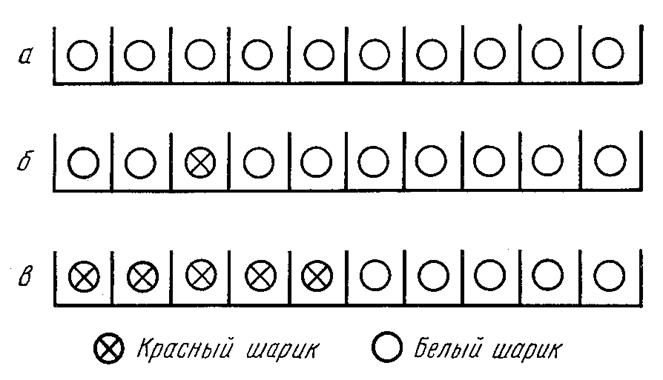
Рисунок 69 – Схема, иллюстрирующая понятие энтропии смешения
Пусть в нашем распоряжении имеются 10 одинаковых белых шариков и 10 расположенных в одну линию лунок, отделенных друг от друга промежутками. В каждую лунку можно положить только один шарик. Это – грубая модель кристаллической решетки, содержащей 10 узлов и 10 атомов какого-либо одного сорта.
Интересующее нас состояние системы – 10 шариков лежат в 10 лунках (рисунок 69а). Ясно, что 10 одинаковых шариков в 10 лунках можно разместить единственным способом. Состояние системы осуществляется этим единственным способом, поэтому W=1 и S=О.
Предположим теперь, что среди 10 шариков оказался один красный. Мы можем поместить красный шарик в любую из 10 лунок, например в третью слева (рисунок 69б). Таким образом, в нашем распоряжении 10 различных способов размещения 10, шариков (9 белых и 1 красный) по 10 лункам: W=10. Следовательно, S=klnW=3,2.10-23 дж/град (7,6.10-24 кал/град).
Термодинамическая вероятность выросла в 10 раз, а энтропия всего на 3,2.10-23 дж/град (7,6.10-24 кал/град). Если бы у нас было не по 10 шариков и лунок, а по N = 6.1023 (один грамм-атом твердого тела) и среди этих шариков был один красный шарик, то W=6.1023, а S~7,5.10-22 дж/град (1,8.10-22 кал/ град) - все еще очень малая величина.
Очевидно, если среди 10 шариков оказались бы 2 красных, то число возможностей размещения шариков по лункам еще возросло бы. Теперь W равнялось бы числу способов размещения двух одинаковых шариков по 10 лункам. В общем случае число сочетаний из n элементов по k
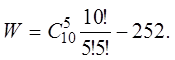
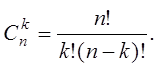(207)
В нашем случае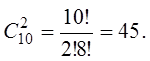 
Таким образом, состояние нашей системы, если она содержит два красных шарика, можно осуществить уже 45 способами: W= 45.
Ясно, что W будет иметь максимум, если взять 5 белых и 5 красных шариков. В этом случае Следовательно, термодинамическая вероятность выросла в 252 раза по сравнению со случаем, когда все шарики одинаковы.
Очевидно, что замена части белых шариков красными моделирует образование бинарного твердого раствора. Таким образом, можно рассчитать изменение энтропии при образовании раствора – энтропию смешения.
Наложим теперь на нашу систему, состоящую из 5 белых и 5красных шариков в 10 лунках, дополнительное условие: потребуем, чтобы все 5 красных шарика были расположены подряд левее белых (рисунок 69в). Очевидно, что состояние осуществляется опять-таки единственным способом: W=1, т. е. S=0, несмотря на то, что в системе есть шарики двух сортов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.