В качестве примера рассмотрим вывод формулы для равновесной концентрации вакансий.
Пусть кристалл содержит n узлов, в том числе nv вакантных, и, следовательно, (n-nv) – занятых атомами какого-либо одного сорта. Если принять свободную энергию кристалла без вакансий равной нулю, то свободную энергию кристалла с вакансиями можно записать в виде
![]() (209)
(209)
где ΔHv – изменение теплосодержания кристалла при образовании одной вакансии,
ΔSv – изменение энтропии кристалла при образовании nv вакансий.
Предполагается, что тепловой эффект не зависит от количества вакансий и при образовании первой вакансии – такой же, как и для любой последующей. Очевидно, ΔHv>0, поскольку для образования вакансий требуется затрата энергии (тепло поглощается).
Из приведенных соображений следует, что ΔSv>0, так как введение вакансии (а так же атома другого сорта) означает увеличение беспорядка в кристалле. Изменение энтропии при введении nv вакансий можно оценить по формуле
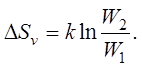 (210)
(210)
где W1 и W2 соответствует числам способов осуществления состояния системы без вакансий и содержащей nv вакансий.
Очевидно, если не рассматривать другие источники разупорядочения, W1=1 (n одинаковых атомов по n узлам можно разместить единственным способом). Величина W2 равна числу способов размещения nv вакансий по n узлам. Согласно (207),
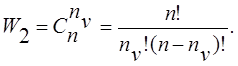 (211)
(211)
Подставляем (211) и (210) в (209) и находим равновесное
количество вакансий (![]() ) из условия
минимума свободной энергии:
) из условия
минимума свободной энергии:
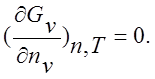 (212)
(212)
Из формулы (212) получаем
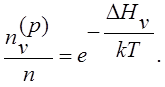 (213)
(213)
При выводе формулы (213) мы не учитывали колебательную энтропию (S*). Иначе
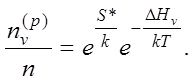 (214)
(214)
Поскольку G = G (Р, Т) то при изменении в системе температуры Т и давления Р равновесие нарушается, т.е. происходят фазовые превращения.
Эренфестом была
предложена классификация фазовых переходов. К фазовым переходам первого рода
относятся переходы, сопровождающиеся скачкообразным изменением энтропии S
и объема V, т.е. первых производных G по температуре и давлению ![]()
Со скачком энтропии связан тепловой эффект ΔH=TΔS, т.е. такие переходы сопровождаются выделением или поглощением тепла. Связь между равновесными значениями T и P при переходе описывает уравнение Клапейрона-Клаузиуса
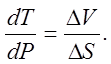 (215)
(215)
Фазовые переходы второго
рода сопровождаются скачком теплоемкости при постоянном давлении ср,
коэффициента объемного расширения 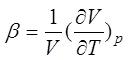 и сжимаемости
и сжимаемости 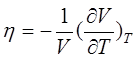 , т.е. вторых производных G:
, т.е. вторых производных G:
![]() (216)
(216)
Напротив, ΔS=ΔV=0. Соответственно и ΔH=0 – фазовые переходы второго рода, происходят без теплового эффекта.
Примерами фазовых переходов первого рода могут служить агрегатные и аллотропические превращения, примерами переходов второго рода - превращения порядок – беспорядок в сплавах типа β-латуни, переход из ферромагнитного в парамагнитное состояние (магнитное превращение), переход в сверхпроводящее состояние и др.
Отметим, что при фазовых переходах первого рода состояние системы меняется скачком, при переходах второго рода – непрерывно, однако возникновение нового элемента симметрии (например, симметрии в заполнении узлов решетки атомами при упорядочении или симметрии в ориентации спинов при магнитном превращении) происходит скачкообразно.
При переходе к сплавам появляется новая термодинамическая переменная – концентрация, являющаяся важнейшей характеристикой сплава.
Для бинарного сплава
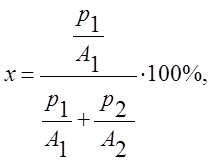 (217)
(217)
где х – % (ат.),
р – % (по массе),
А – атомные массы.
Например, при содержании в стали 1% (по массе) С
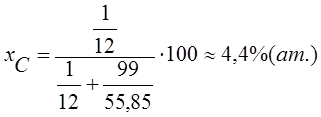 (218)
(218)
В некоторых случаях, когда компоненты сплава отличаются валентностью, пользуются величиной электронной концентрации (С):
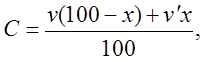 (220)
(220)
где v – валентность растворителя;
v` – валентность растворенного элемента;
х – атомный процент растворенного элемента.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.