Плоскости габитуса частиц, имеющих правильную огранку, параллельны определенным кристаллографическим плоскостям исходной фазы; кристаллическая решетка новой фазы закономерно ориентирована относительно решетки исходной фазы; наконец, сами частицы обычно имеют закономерное взаимное расположение, часто образуя одно-, двух-, или трехмерные сетки.
Такое расположение при распаде твердых растворов бывает настолько строгим, что в дифракционной картине (рентгеновской или электронной) рядом с определенными Вульф - Брэгговскими отражениями могут возникать сателлиты – признак квазипериодической или «модулированной» структуры.
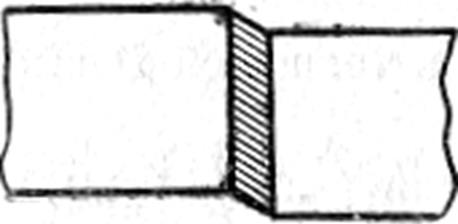

Рисунок 77 – Пластина выделения, проходящая через весь кристалл исходной фазы (а), и образование кристалла внутри объема исходной фазы (б):
у края пластины внутри исходного кристалла условно показано поле упругой деформации
Морфология гетерогенной структуры, а также дисперсность структуры определяются совместным действием упругой и поверхностной (межфазовой) энергией. А. Л. Ройтбурд и А. Г. Хачатурян дали наиболее общее решение задачи об упругой энергии частицы, рассматриваемой как изолированное когерентное включение в упруго-анизотропной матрице. Минимальная упругая энергия получается для включения пластинчатой формы. Поверхность пластины совпадает с той плоскостью кристалла, которая меньше всего искажается при превращении. Фактор поверхностной энергии препятствует превращению включения в бесконечно тонкую (и бесконечно протяженную) пластину, поскольку поверхностная энергия минимальна для включения равноосной формы.
Выражение для упругой энергии кристалла, содержащего когерентное пластинчатое включение (или систему включений), состоит из двух членов: первый пропорционален объему включения, и поэтому, складывается с объемной химической свободной энергией, второй связан с деформацией у торцов пластины и формально может быть интерпретирован как энергия дислокационной петли, охватывающей включение по его периметру. Первый член равен нулю, если деформация при превращении есть деформация с инвариантной плоскостью и плоскость габитуса параллельна инвариантной плоскости. Деформация с инвариантной плоскостью означает, что в процессе превращения, которое при изменении кристаллической структуры можно рассматривать как «структурную» деформацию, имеются плоскости, в которых расположение атомов не изменяется и которые сами не поворачиваются. Простейшей моделью деформации с инвариантной плоскостью может служить движение игральных карт в колоде (скольжение). Деформацией с инвариантной плоскостью является двойникование в кристаллах, а также подробно рассматриваемое ниже мартенситное превращение. Второй член должен быть равен нулю, если пластина включения проходит через весь кристалл (рисунок 77а). Если пластинчатое выделение оказывается внутри кристалла, го поле упругих искажений возникает у торцов пластины (см. рисунок 77б) и величина упругой энергии будет пропорциональной периметру пластинчатого выделения.
Для пластины в виде диска радиусом R и толщиной D имеем
Еупр = β D /4π( - lnD/R +21n2 -1/2 ) 2πR, (223)
β~με20 (224)
где μ – модуль упругости;
ε0 – деформация, характеризующая переход от исходной к кристаллической структуре новой фазы.
Энергию Еупр; можно представить как энергию линейного натяжения струны длиной 2πR с коэффициентом линейного натяжения.
δ=βD2 /4π(-lnD/R +2ln2- ½) ~ μb2, (225)
где b=Dεо имеет смысл вектора Бюргерса.
Для того чтобы выяснить пределы применимости предположения о том, что форма включения (пластина толщиной D и длиной L) определяется условием минимума упругой энергии, оценим порядок величины Еупр из уравнения (222)
Eyпр~με 2 0LD2, (226)
Энергия поверхностного натяжения пропорциональна поверхности включения и без учета влияния торцов пластины имеет порядок αL2 , где α – коэффициент поверхностного натяжения.
Примем, что когда сумма поверхностной и упругой энергии минимальна, порядок величины для упругой и для поверхностной энергий один и тот же:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.