Фазовые превращения. Общие положения и закономерности, классификация. Аллотропические превращения. Полиморфизм, страница 16

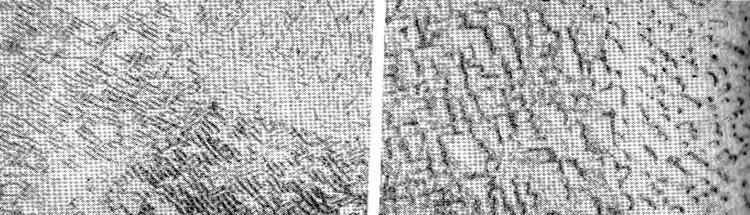
а                                                         б

а – сплав 40 ат.% Fe: выделение Fе-фазы в окружении NiAl-матрицы;

б – сплав 70 ат. % Fe выделение NiAl-фазы в окружении мягкой

Fе-матрицы. ´1000

Рисунок 79 – Влияние различия жесткости исходной (матричной) фазы и новой (фазы выделения} на форму частицы в сплавах Fe–Ni–A1 после закалки и отжига 100 ч при 800°С

Условие минимума энергии упругой деформации при образовании новых фаз в твердом состоянии определяет не только форму отдельных частиц, но и их взаимное расположение.

В сплаве Ni–Ti (рисунке 81) в условиях сравнительно небольшого пересыщения и небольшого количества избыточной метастабильной у'-фазы (в изоморфной г.ц,к: матрице) ярко проявляется особенность взаимного расположения частиц: первые образовавшиеся частицы (более крупные на фотографии) инициируют образование регулярных рядов последовательно выделяющихся частиц вдоль <100> направлений г.ц.к. матрицы. В гетерогенной структуре в ходе превращения или в конечной структуре имеется еще несколько способов понижения упругой энергии.

Модулированные структуры и упругие концентрационные домены образуются, например, при расслоении твердых растворов. В двойных сплавах Ni-A1, Ni-Ti, Ni-Au, а также в тройных Cu-Ni-Fe, Fe-Ni-A1 и в некоторых других практически очень важных сплавах при распаде твердого раствора с кубической решеткой образуются две новые изоморфные фазы, различные по составу.

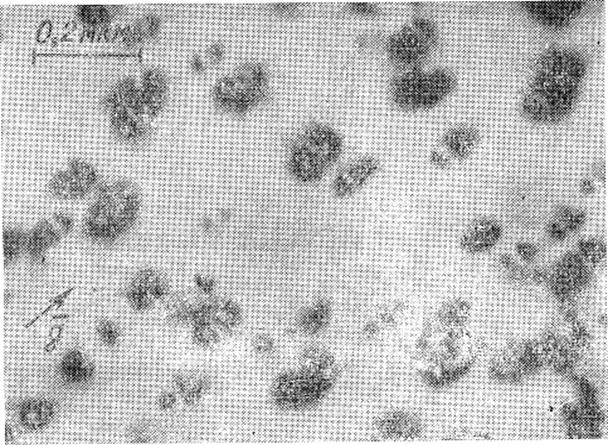
Рисунок 80 – Электронные микрофотографии фольги сплава Fe–Сг–А1, деформационный контраст от сферических выделений фазы FeA1 в ферритной матрице; радиальный характер поля деформации объясняет наличие области нулевого контраста (перпендикулярно к вектору действующего отражения g 002)

Примем, что концентрационная зависимость периода решетки подчиняется правилу Вегарда, т. е.

                а=а₀ (1 + g_oс) .                                          (230)

где а_о – период решетки одного из чистых компонентов;

q_o – линейный коэффициент концентрационного расширения решетки;

с – концентрация второго компонента.

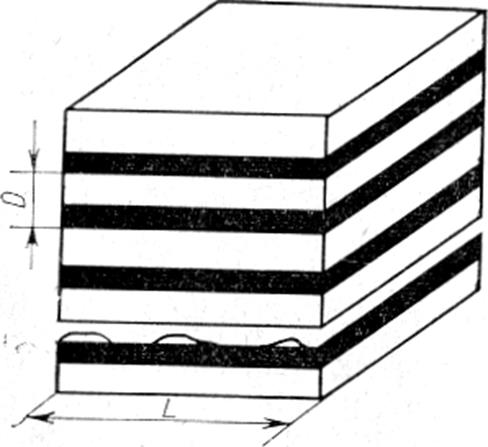
Различия состава и соответственно периодов решетки сопрягающихся фаз должны приводить к возникновению напряжений. Можно показать, что в отношении упругой энергии более выгодно образование комплексов из перемежающихся пластин обогащенной и обедненной фаз (рисунке 82), чем независимое образование пластин тех же фаз. Соотношение толщин этих пластин в комплексе определяется диаграммой состояния (правило рычага).

Если справедливо правило Вегарда, то любое перераспределение атомов компонентов, включая перераспределение, приводящее к образованию двух изоморфных твердых растворов, не вызывает изменения заданного объема (объема комплекса). Поэтому на достаточно большом расстоянии от комплекса (больше, чем период внутренней неоднородности комплекса D) поле упругих напряжений в матрице равно нулю. Если пластины комплекса не выходят на поверхность кристалла, то упругие напряжения должны быть в слое, прилегающим к торцам пластин. Толщина этого слоя порядка толщины элементов комплекса D, объем слоя около DL² (L – линейный размер комплекса), величина деформации ~qo∆c (∆с – разность концентраций в фазах – слоях комплекса); плотность упругой энергии ~μq²_o ∆c² и полная энергия

Eупр~μq²_o ∆c² DL².                                 (231)

Рисунок 82 – Упругие концентрационные домены при расслоении

твердого раствора

Из соотношения (231) следует, что упругая энергия тем меньше, чем тоньше концентрационные домены комплекса (Е_упр → 0 при D→0), однако дробление в комплексах должно вызывать повышение поверхностной энергии. Порядок величины

                                                        Е_пов ~аL²L/D(232)

где L² – площадь одной межфазовой границы в комплексе;

L/D – число границ в комплексе.

Выгодная величина периодичности доменов D_o определяется из условия минимума суммы энергий Е_упр и Е_пов:

D_o≈√r₀ /L.(233)