ТАУ 1-1. Математическое описание сигналов и операторов в непрерывных линейных детерминированных системах
Система — набор элементов, которые объединены для достижения технической цели.
Детерминированная система — система с жесткими воспроизводящими характеристиками, которые воспроизводят одинаковые выходные сигналы.
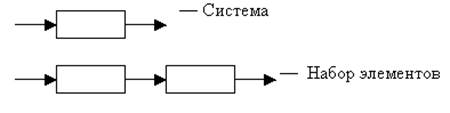 Характерным
признаком для системы будет являться прохождение информации в одном
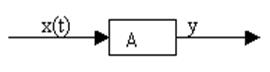
направлении. На входе будут входные сигналы, на выходе — выходные сигналы или переменные.
Характерным
признаком для системы будет являться прохождение информации в одном
направлении. На входе будут входные сигналы, на выходе — выходные сигналы или переменные.
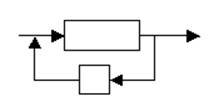 Если
часть информации с вых. возвращается на вход, то в этом случае мы имеем обратную
связь, которая м. б. либо «+», либо «-».
Если
часть информации с вых. возвращается на вход, то в этом случае мы имеем обратную
связь, которая м. б. либо «+», либо «-».
 Если на входе эти сигналы
будут суммироваться, то они «+». Бывают динамичные обратные связи, которые
действуют на переходном времени. Если в системе 2 элемента, то она м. б.
автоматической, если есть обратная связь. В ней осуществляется регулирование по
отклонению. Если нет обратной связи, она получается разомкнутой.
Если на входе эти сигналы
будут суммироваться, то они «+». Бывают динамичные обратные связи, которые
действуют на переходном времени. Если в системе 2 элемента, то она м. б.
автоматической, если есть обратная связь. В ней осуществляется регулирование по
отклонению. Если нет обратной связи, она получается разомкнутой.
Математической основой для описания и анализа элементов системы м. б. ДУ.
ДУ м. б. линейные и нелинейные.
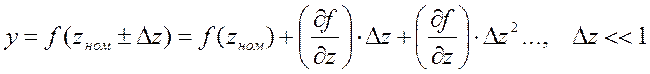
Линеаризация характеристик элементов и систем, т.е. разложения в ряд, либо графически и находим коэффициенты.
Найдем простейшие функции. Возьмём функцию Дерака.
![]()
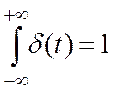
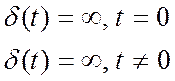
Воспользуемся интегральной зависимостью:
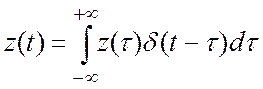 , t —
фиксированные точки, τ — переменные точки
, t —
фиксированные точки, τ — переменные точки
С помощью функции Дирака можно зафиксировать значения сложной функции.
Сложную функцию можно выразить ч/з набор импульсов, изменяя значения времени, задавая функцию Дирака в различных точках временной оси, мы можем сформировать любую амплитуду сигнала.
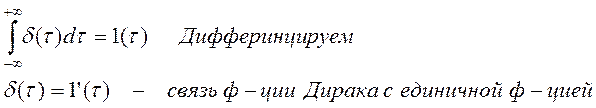
ТАУ 1-2 Гармоническая
функция: ![]() . На выходе будут изменения либо по фазе,
либо по амплитуде.
. На выходе будут изменения либо по фазе,
либо по амплитуде.
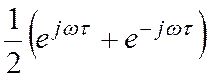
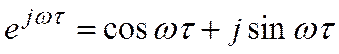
Эти функции являются основой для исследования временных, частотных характеристик.
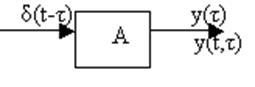 На
выходе для функции Дирака получим:
На
выходе для функции Дирака получим:
g(t,τ)=A δ(t- τ) — функция реакции системы на функцию Дирака (весовая функция).
Весовая функция характеризует св-ва либо элемента, либо самой системы.
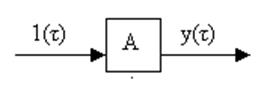 Если
на входе:
Если
на входе:
h(τ)=A×1(τ) — переходная функция
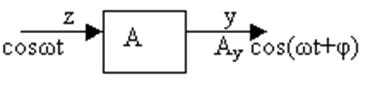
Если на входе cosωt, то на выходе:
y(ωt)=Acosωτ
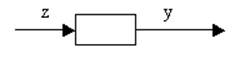
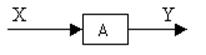
Пусть есть оператор
|
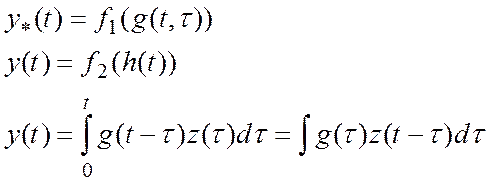
Можно найти зависимости вых. величины от сигналов ч/з промежуточные состояния.
 В
этом случае, если представить входной сигнал
В
этом случае, если представить входной сигнал 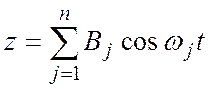 , то
на выходе будет иметь такую же сумму
, то
на выходе будет иметь такую же сумму 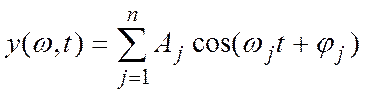
Для того, чтобы охватить весь спектр этих составляющих надо включить еще и мнимые состояния: z(jωt) и y(jωt). Связь м/ду частотными характеристиками:
y(jω)=WA(jω)z(jω)
передаточная (частотная функция) — обозначает передачу входного сигнала на выход.
Преобразование Лапласа охватывает мнимые составляющие.
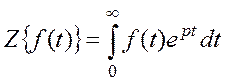 — отражает мнимые составляющие.
— отражает мнимые составляющие.
|
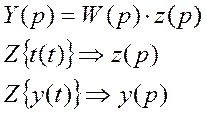
ТАУ 1-3
Если сделать преобразование Лапласа весовых функций
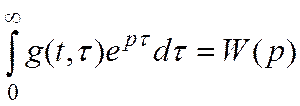 — передаточная функция.
— передаточная функция.
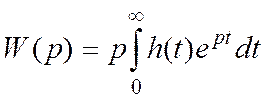 — преобразование Карсона.
— преобразование Карсона.
![]()
Если сделать преобразование Фурье:
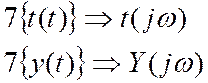
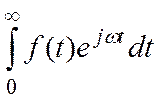
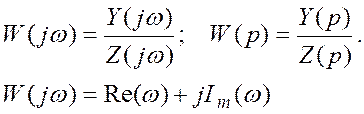
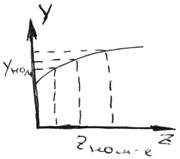
Задаёмся
значениями частоты ![]() , находим
, находим ![]() и
чертим график.
и
чертим график.
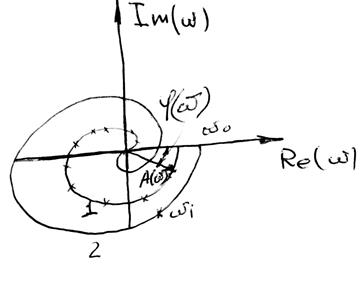 Если
с начала координат провести вектор в точку
Если
с начала координат провести вектор в точку ![]() ; длинна
вектора коэффициент передачи системы на данной частоте, а угол
; длинна
вектора коэффициент передачи системы на данной частоте, а угол ![]() сдвиг фаз на данной частоте.
сдвиг фаз на данной частоте.
Амплитудная
характеристика ![]()
Фазовая
характеристика 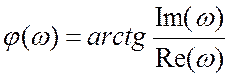
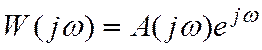
ТАУ 2-1. Математическое описание сигналов в непрерывных линейных стохастических системах.
Для них характерным понятием является случайный процесс, который может появляться на входе, на выходе, на выходе, либо и там и там одновременно.
Для оценки таких составляющих необходимо знать функции плотности распределения, тогда можно найти случайные величины через эти плотности , через интервалы свертки (с функцией распределения).
Прогнозирование следующего значения на основе предыдущего имея некоторую зависимость, следовательно существует некоторая база для создания теории.
Например, спектральный метод:
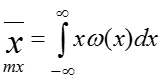 — среднее математическое отклонение
— среднее математическое отклонение
![]() — дисперсия
— дисперсия
Для стационарных процессов число случайных точек можно заменить средним числом на интервале наблюдения
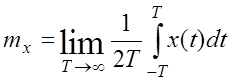
Получаем среднее значение и делим на число точек
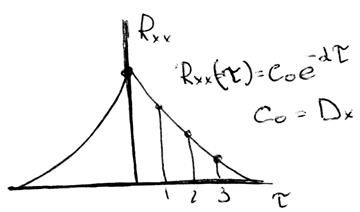
Меру связанности назвали корреляционной связью. Изучается коэффициент корреляции для одной и той же выборки
![]() , τ=0,1,2…
, τ=0,1,2…
Аргументы второй составляющей сдвинуты на τ. Последовательно задаемся значениями τ и находим коэффициенты для всех возможных значений.
τ
=0: 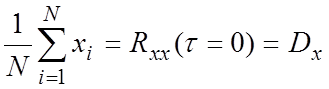
τ =1: 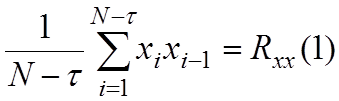
τ =2: 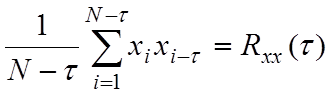
Можно найти целое семейство коэффициентов, которые будут связью одного и того же процесса при сдвиге.
 Взаимокорреляционная
функция:
Взаимокорреляционная
функция:
M{x(t)y(t+τ)}=Rxy(τ)
Rxy(τ)=Rxy(τ)—взаимокорреляционная функция
Если τ =0, мы находим дисперсию входной и выходной величины Dxи Dyсоответственно.
А— математическая функция, которая описывает ТАУ 2-2 поведение системы, внутреннее состояние, свойства во временной области. Можно воспользоваться весовой функцией.
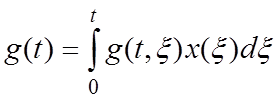 — позволяет через весовую функцию, зная
изменение x на интервале, можно рассчитать значение y в
соответствующий момент времени. Составим корреляционную функцию вида:
— позволяет через весовую функцию, зная
изменение x на интервале, можно рассчитать значение y в
соответствующий момент времени. Составим корреляционную функцию вида:
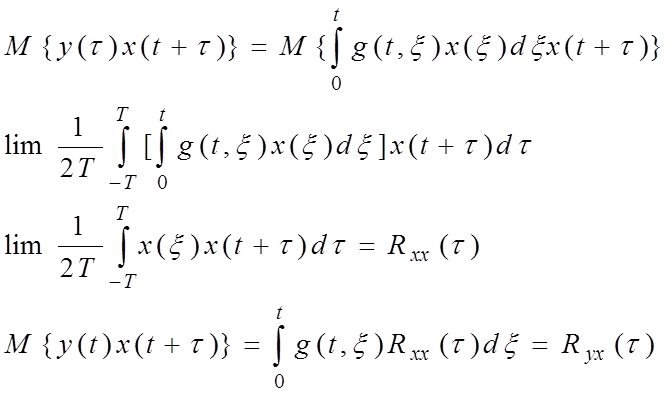
 Взаимокорреляционные
и автокорреляционные функции связаны через интеграл и через весовую функцию,
которая описывает внутренние процессы.ъ
Взаимокорреляционные
и автокорреляционные функции связаны через интеграл и через весовую функцию,
которая описывает внутренние процессы.ъ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.