Свойства и характеристики стационарных случайных процессов.
Во многих случаях возмущения, действующие на различные каналы объекта, не удается стабилизировать. На некоторых объектах крайне нежелательна подача специальных апериодических возмущений. В этих случаях для определения дин.хар-к могут быть использованы статистические хар-ки сигналов на входе и выходе. Задача разбивается на 2 этапа: 1)Определение статист. характеристик случ. процессов, действующих на объект;2) Опред-е по ним дин.хар-к.
Каждый процесс характер-ся определ-ым кол-вом технологич-х
параметров, многие из которых изменяются по случайному закону, т.е. совершают
колебательные движения около среднего положения. Если статические хар-ки
неизменны во времени, то такие процессы наз. стационарными. Выделение статич-х
хар-к производится путем усреднения ординат сл. процессов разл-ми методами.Если
результат усреднения не зависит от способа усреднения и от вида реализации, то
такие сл. стац. процессы называют эргодическими. Осн-й статической хар-кой
является мат.ожидание 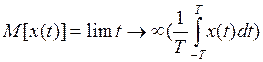 , t- время реализации сл.процесса.
Остальные хар-ки удобно описывать по центрированным значениям сл.процесса,
которые получаются путем”-” из текущих ординат. Вся необх-я информация
заключается в корреляционных функциях:
, t- время реализации сл.процесса.
Остальные хар-ки удобно описывать по центрированным значениям сл.процесса,
которые получаются путем”-” из текущих ординат. Вся необх-я информация
заключается в корреляционных функциях: 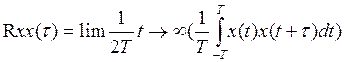 ,
,![]() - время сдвига между 2 ординатами.
Физ.смысл
- время сдвига между 2 ординатами.
Физ.смысл ![]() - показывает, насколько величина
сл.процесса при t отличается от величины
процесса через
- показывает, насколько величина
сл.процесса при t отличается от величины
процесса через![]() .Имеет свойства: 1)четный характер:
.Имеет свойства: 1)четный характер:
![]() ;2)
;2) ![]() ;3)
;3) ![]() ,
,![]() ;4)
;4) ![]()
![]() .Взаимосвязь между 2
сл.процессами определяется взаимокоррел. функцией
.Взаимосвязь между 2
сл.процессами определяется взаимокоррел. функцией 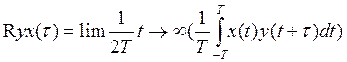 - определяет связь входа с выходом.
Свойства:
- определяет связь входа с выходом.
Свойства:
1)нечетный характер: ![]() ;2)
;2) ![]()
![]() .Если исследуются
частотные характеристики, то используется спектральная плотность
.Если исследуются
частотные характеристики, то используется спектральная плотность ![]() . По преобразованию Фурье от
коррел.функции
. По преобразованию Фурье от
коррел.функции 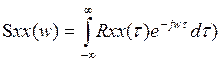 ,
,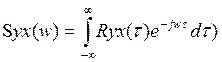 .При
обратном преобразовании Фурье:
.При
обратном преобразовании Фурье: 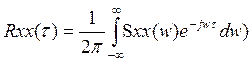 Физ. cмысл:
Физ. cмысл: ![]() -
определяет мощность сл.процесса в каком-либо интервале частот. Принимаем время
-
определяет мощность сл.процесса в каком-либо интервале частот. Принимаем время![]() в выражении для
в выражении для ![]() и
получаем:
и
получаем: 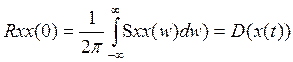 .Связь между спектр. плотностью и входным
сл.процессом, который проходит через объект с перед. функцией
.Связь между спектр. плотностью и входным
сл.процессом, который проходит через объект с перед. функцией ![]() :
:![]() .Преобразуем:
.Преобразуем: 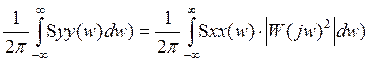
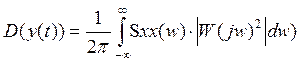 -это дисперсия вых.
сигнала
-это дисперсия вых.
сигнала
Для ее вычисления применяются методы приближенного
интегрирования 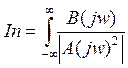 .
.
![]()
![]() .В
общем случае при отсутствии нулевых корней у А
.В
общем случае при отсутствии нулевых корней у А 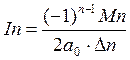 ,
,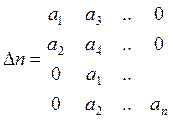
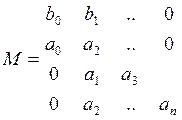 .
.
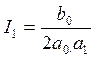 ,
,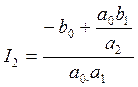 ,
,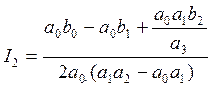 .
.
АЭП 21. Динамическое торможение АС двигателя
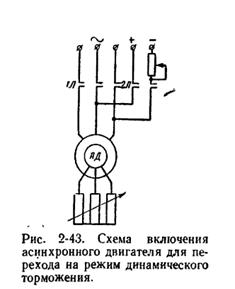 Динамическое торможение
двигателя осущ-ся включением обмотки статора на сеть постоянного тока, обмотка
ротора при этом замыкается на внешнее сопротивление. Для перехода из двигат-о
режима в режим дин. тормож-я контактор 1Л отключает статор от сети пер. тока, а
конт-р 2Л присоединяет обмотку статора к сети пост-го тока. Для ограничения тока
и получения различных характ-к в цепи ротора ставится сопротивление.Проходя по
обмотке статора, пост. ток образует неподвижное поле, основная волна которого
дает синусоид-е распределение индукции. Во вращающемся роторе возникает перем-й
ток, создающий свое поле, которое неподвижно относ-но статора. В результате
взаимодействия суммарного магнитного потока с током ротора возникает тормозной
момент, который зависит от и.с. статора, Rротора и
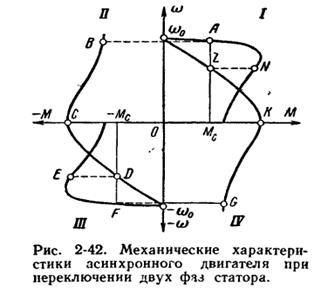
скорости двигателя.Мех. характеристики проходят через начало координат, т.к.при
скорости, равной нулю, торм. момент = 0.Величина Мкрит
пропорциональна квадрату приложенного к статору напряжения и ↑ с ростом U.
Крит-е скольжение зависит от R,включенного в ротор.
Динамическое торможение
двигателя осущ-ся включением обмотки статора на сеть постоянного тока, обмотка
ротора при этом замыкается на внешнее сопротивление. Для перехода из двигат-о
режима в режим дин. тормож-я контактор 1Л отключает статор от сети пер. тока, а
конт-р 2Л присоединяет обмотку статора к сети пост-го тока. Для ограничения тока
и получения различных характ-к в цепи ротора ставится сопротивление.Проходя по
обмотке статора, пост. ток образует неподвижное поле, основная волна которого
дает синусоид-е распределение индукции. Во вращающемся роторе возникает перем-й
ток, создающий свое поле, которое неподвижно относ-но статора. В результате
взаимодействия суммарного магнитного потока с током ротора возникает тормозной
момент, который зависит от и.с. статора, Rротора и
скорости двигателя.Мех. характеристики проходят через начало координат, т.к.при
скорости, равной нулю, торм. момент = 0.Величина Мкрит
пропорциональна квадрату приложенного к статору напряжения и ↑ с ростом U.
Крит-е скольжение зависит от R,включенного в ротор.
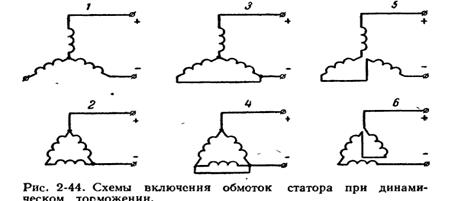 Питание обмоток статора
асинх-ого дв-ля может производится от сети пер. тока через полупроводниковый
выпрямитель В.Анализ работы проводится, считая, что статор питается не пост. U, а
эквивал. Трехфазным перем. током. Амплитуда и.с., создаваемая перем. током:
Питание обмоток статора
асинх-ого дв-ля может производится от сети пер. тока через полупроводниковый
выпрямитель В.Анализ работы проводится, считая, что статор питается не пост. U, а
эквивал. Трехфазным перем. током. Амплитуда и.с., создаваемая перем. током: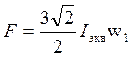 ,где w-число последовательно
соединенных витков фазы статора.Намагничивающая сила, создаваемая постоянным
током, пропорцион-а величине постоянного тока, числу витков фазы статора и
зависит от схемы соединения.Напр., при соединении статора в звезду и прохождении
,где w-число последовательно
соединенных витков фазы статора.Намагничивающая сила, создаваемая постоянным
током, пропорцион-а величине постоянного тока, числу витков фазы статора и
зависит от схемы соединения.Напр., при соединении статора в звезду и прохождении
постоянного тока только по
двум фазам и.с. пост. тока, равна![]()
 Исходя из равенства,
определяют значение эквив. перем. тока:
Исходя из равенства,
определяют значение эквив. перем. тока:![]()
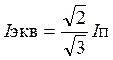
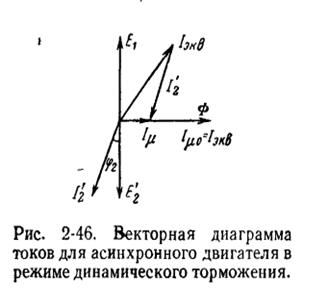
По току можно построить упрощенную векторн. диаг-му
На диаграмме Iµ - ток намагничивания, I2’ - вторичный ток, приведенный к статору, Iэкв – первичный эквивалентный ток, Е2’, E1 – соответственно вторичная приведенная и первичная э.д.с.
Намагничивающий ток Iμ определяется геометрической суммой
эквивалентного тока Iэкв и вторичного приведенного к статору тока I2’. Величина эквивалентного тока не зависит от скорости
вращения ротора, тогда как с изменением скорости изменяется вторичный ток.
Конец вектора тока Iэкв при уменьшении скорости вращения ротора будет перемещаться
по окружности вправо и при неподвижном роторе вектор Iэкв
совпадет с Iμ так как вторичная э. д. с. и
соответственно вторичный ток окажутся равными нулю. Поэтому при малых скоростях
вращения ротора и сравнительно большом эквивалентном токе двигатель в режиме
динамического торможения оказывается с сильно насыщенной магнитной системой.
Наоборот, при больших скоростях и том же эквивалентном токе магнитная система
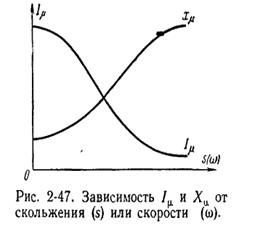
будет ненасыщенной. Примерная зависимость ![]() приведена
на рис. 2-47.
приведена
на рис. 2-47.
В связи с явлением насыщения магнитной системы не остается постоянной и реактивность намагничивания Хμ (рис. 2-47)
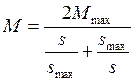 (2.49)
(2.49)
Уравнение (2-49) по своей структуре аналогично уравнению механической характеристики асинхронного двигателя в режиме.
Отметим, что критическое скольжение в двигательном режиме существенно больше критического, скольжения в режиме динамического торможения при том же сопротивлении цепи ротора, т. е.
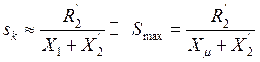 .
.
Вследствии того, что ![]()
Кроме того, в реальных условиях в связи с уменьшением Хµ и ротором Iэкв smax не остается постоянным для различных Iэкв; следует есть также, что кривая
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.