Мы зададимся разными начальными условиями: X(0),
такими, что ошибка (X(0)
- )<δ.
(X(к+1) - 
)<ε - число, которым
мы можем задаться сами произвольно.
Когда при условии 
, а 
в этом случае асимптотная система
устойчива.
На сегодняшний день есть понятие, когда U(к)
0.
Возьмём сночало скалярную систему:
Х(к+1)=А*Х(к)+В*U(к)
U(к)=0; Х(к+1)= А*Х(к)
X(0)
0; Х(к+1)= a*Х(к)
X(1)=a*X(0)
X(2)=a*X(1)=a^2*X(0) … X(k)=a^k*X(0)
; X(k)
0.
Когда, а=0, то, а^к не играет значения.
Когда, а<1, то, а^к будет уменьшаться, и 
<1 не играет роли, какой знак имеет а в
данном случае.
Сделаем Z преобразование:
Z*X(z)=a*X(z)
(Z-a)*X(z)=0
Мы видим, что мы можем Z-a=0 
Z=a. Когда <1 система устойчива.
Характеристическое уравнение для заданной системы:
a0*Z^n+a1*Z^(n-1)+…+an=0.
Когда хотя бы один корень будет > 1, то наша система неустойчива.
Если хотя бы один корень будет = 1, то система находится на границе устойчивости.
Для матрицы А необходимо найти собственные числа, и когда они будут по модулю < 1, то наша система является устойчивой.
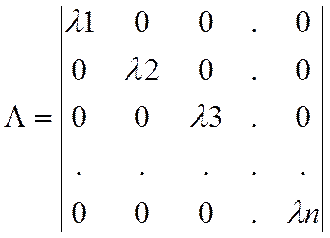
ТАУ 9. Критерий устойчивости нелинейных систем.
Критерий Попова. Поповым был предложен критерий на основе исследования частотных хар-к нелинейных систем с одной нелинейностью. Эта нелинейность может иметь сложную форму. Он предложил выделить сектор отсечки прямой линии, внутри которой будет находиться нелинейная хар-ка.
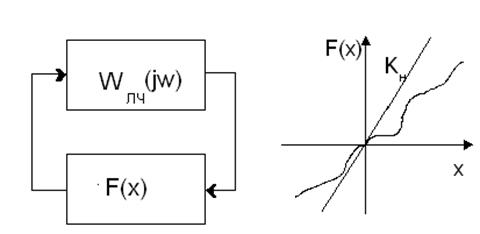Кн – коэффициент наклона линии.
Нелинейность находится в зоне [0,Кн].
Далее была доказана теорема:
Нелинейная система приведенной структуры при условии, что нелинейность можно разместить в секторе вида [0,Кн] будет абсолютно устойчива если справедливо следующее неравенство
;
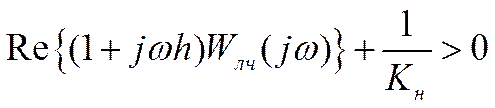h– свободный коэффициент, согласующий условия (произвольный положительный коэффициент).
Выделим вещественную часть из частотной составляющей:
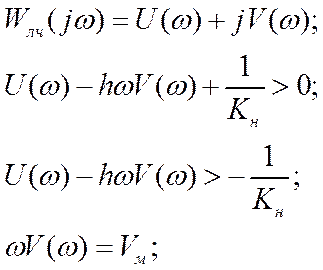
Мы
можем построить частотную хар-ку, которая соответствует павой части последнего
неравенства, задаваясь частотами. Затем откладываем точку с координатами (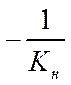
,0) и если можно провести через эту точку
линию или подобрать такой h, чтобы эта линия проходила слева от частотной хар-ки
и не пересекала её, то в этом случае система будет абсолютно устойчива.
ТАУ 10. Построение переходных процессов для линейных непрер. систем.
1) Численные методы. Этот метод используется с применением ЭВМ так как возникают проблемы с решением д.у. высокого порядка:
;
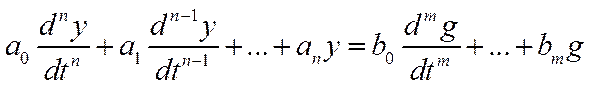y – выходное воздействие, а g – входное.
Примем
, затем подставим в правую часть.
2) Аналитические методы (остановимся на частных случаях):
Возьмём случай когда коэффициенты b0, b1,…bm-1. В этом случае решение будет состоять из вынужденного и общего решения
. 
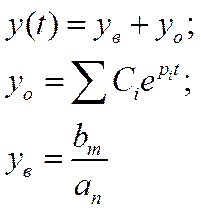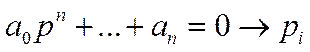
Если есть начальные условия, то можно найти постоянные интегрирования, а следовательно имеем аналитическое решение д.у.
3) Операторный способ
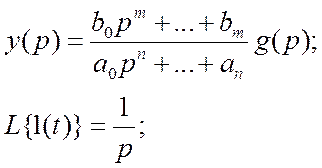
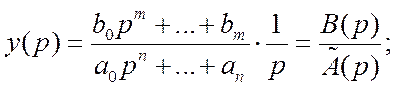
Далее по таблице можно найти обратный переход:
Если
найти корни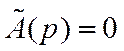 
pi=0,p1…
Воспользуемся формулой разложения:
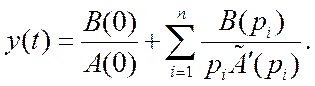
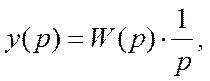
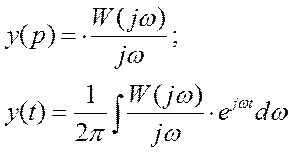- обратное преобразование
Фурье .
ТАУ 11. Построение переходных процессов для линейных дискретных систем.
Рассмотрим импульсную передаточную функцию звена или системы. Пусть мы имеем звено, кот. описывается в форме передаточной ф-и или в форме весовой ф-и.
Вводим квантователь на входе и выходе системы. Для простоты, считаем что квантователи синхронизированы. U(t) – входной сигнал и если квантователи идеальны, то на выходе мы имеем
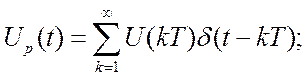
y(t) –выход звена:
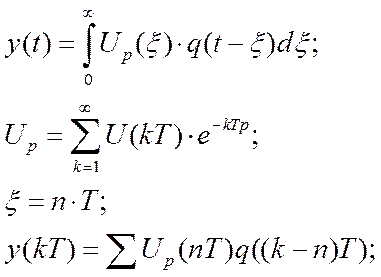
Если сделать некоторые преобразования и произвести ряд замен, то получим:
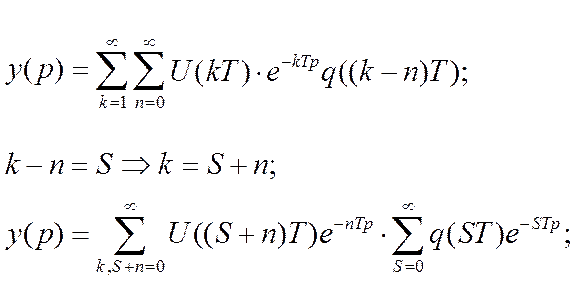
в результате получили две отдельные суммы. Если сделать подстановку
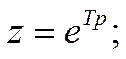
получим
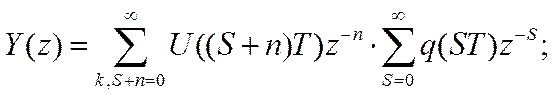
последняя часть выражения и будет импульсной передаточной ф-ей W(z).
Имеем
такую же форму как и для преобразования Лапласа. W(z) –
импульсная передаточная ф-я, её можно получить на основе весовой ф-и или на
основе z-преобразования 
ТАУ 12-1. Критерии качества регулирования.
Прямые критерии кач-ва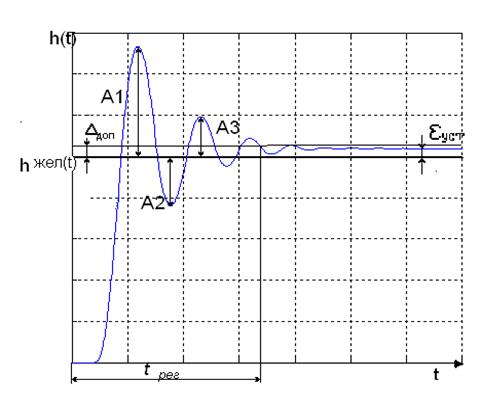
εуст - установившаяся ошибка.
∆доп – допустимый(доверительный) интервал ошибки: если допустимый интервал не задан, то по умолчанию мы принимаем его 5% от hжел.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.