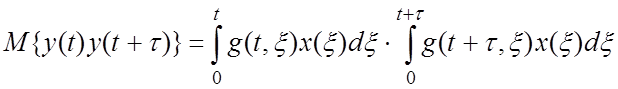
Перейдем в частотную область:
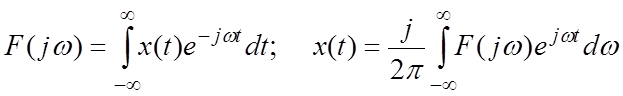
Возьмем модуль F(jw)
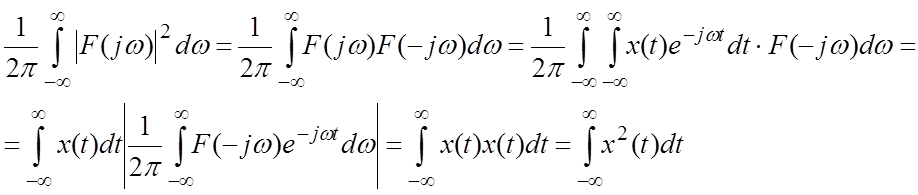
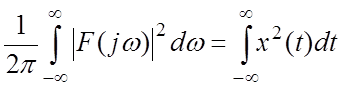 — формула Релея
— формула Релея
ТАУ 2-3
Получим усредненные значения переменных в реальном времени:
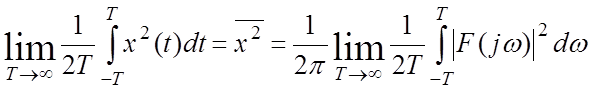
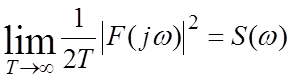 — усредненное квадратичн. значение
частотных свойств
— усредненное квадратичн. значение
частотных свойств
спектральная ф-я
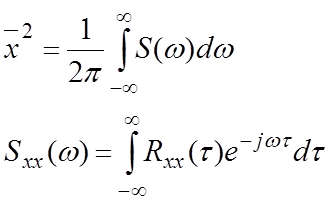
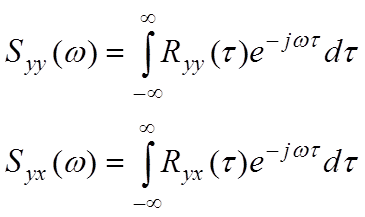
В частотной области характерной является спектральная функция.
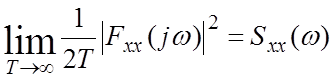 — вход
— вход
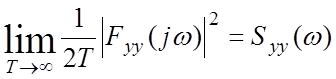 — выход
— выход
![]() Выходной сигнал:
Выходной сигнал:![]()
Оператор в частотной области
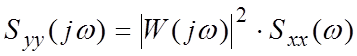
![]()
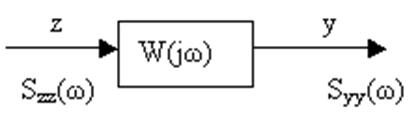 Syy=|W(jω)|2Szz
Syy=|W(jω)|2Szz
Syz=W(jω)Szz
Если речь идет о линейных системах, то для них характерно свойство, что любой сигнал можно разложить на элементарные составляющие и представлен в виде их суммы:
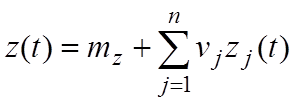
mz — математическое ожидание для z(t)
zj — элементарные функции Дирака
vj — коэффициенты
Такое представление случайного сигнала было сделано Пугачевым
ТАУ 3-1. Математическое описание дискретных систем.
|
Пусть описывается импульсной передаточной функцией
![]()
![]()
![]()
![]()
![]() U X
Y
U X
Y
X– вектор переменных состояния. Чаще линейные системы описываются:
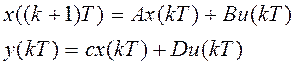
Пусть у есть передаточная функция
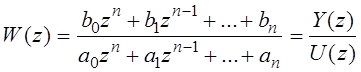 ;
; 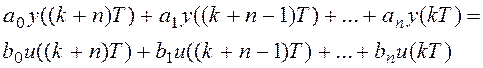
Пусть
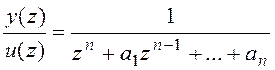
В реальном времени:
![]()
![]() — ввели новую переменную
— ввели новую переменную
Будем рассматривать на следующем такте:
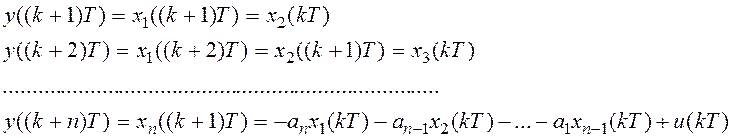
Получим следующую систему уравнений:
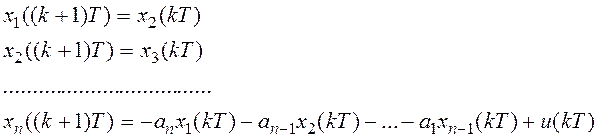
Эту систему можно записать в матричной форме:
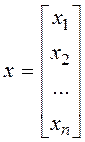 ,
, 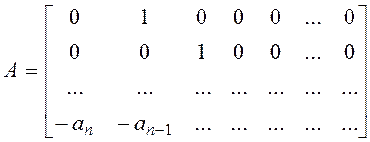 ,
, 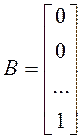
Тогда получим:
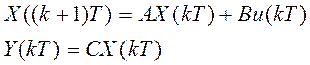 , где
, где ![]()
Таким образом, мы ввели новую систему переменных. Есть след. Переход к переменным состояния:
![]()
![]()
![]()
![]()
![]() U X
Y
U X
Y
Перейдем к общему случаю, когда в числителе тоже есть полином, т.е. в числителе будет столько же коэффициентов, сколько и в знаменателе.
ТАУ 3-2 Т. е. мы имеем: 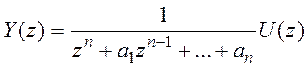
Обозначим
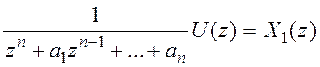
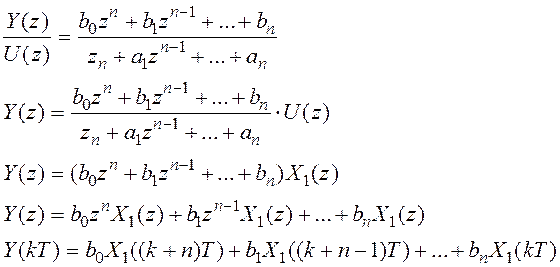
zn — говорит о том, что надо сдвинуть на n тактов.
zn-1 — сдвиг на (n-1) такт и т. д.
![]()
![]()
![]()
![]()
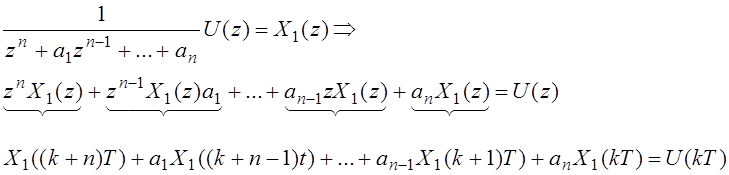
Т. о. для переменных состояния остается такая же модель, которую получили раньше. Есть только одно отличие:
Раньше
было:![]() , а теперь:
, а теперь:![]()
Можно
сказать, что ![]()
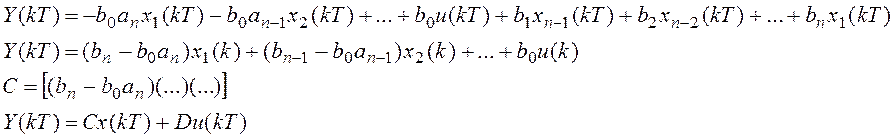 В случае, когда мы имеем импульсную
передаточную функцию, тогда система переменных состояния имеет следующий вид:
В случае, когда мы имеем импульсную
передаточную функцию, тогда система переменных состояния имеет следующий вид:
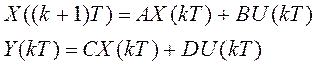
Структурная схема такой системы имеет вид:

 U(kT)
+ X((k+1)T) U(kT) + X(kT)
U(kT)
+ X((k+1)T) U(kT) + X(kT)
![]() X(kT)
X(kT)
Чтобы перевести X(k+1) в X(k) надо домножить на z-1
ТАУ 3-3
Теперь
предположим, что у нас еще есть и запаздывание ![]() , имеем
, имеем ![]()
Пусть у нас есть возможность подбирать (изменять) период квантования Т, чтобы у нас получалось τ=dT, где d— целое число.
Когда запаздывание τ>Т, тогда можно сказать, что модель будет иметь след. вид:
![]()
Можно сказать, что у нас есть запаздывание в управлении на d тактов:
 U((k-d)T)
+ X(kT)
U((k-d)T)
+ X(kT)
|
|
|
|
![]()
![]()
![]()
![]()
![]()
![]()
![]() +
+
 |
 U(kT) U((k-1)T) U((k-d)T)
X(kT)
U(kT) U((k-1)T) U((k-d)T)
X(kT)
…. +
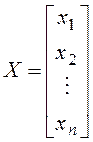 Пусть
Пусть 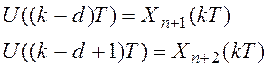 и т. д.
и т. д.
(!)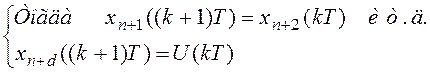
Сумму (!) можно записать в матричной форме:
Имея:
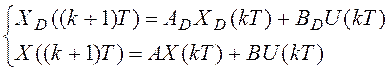
получим более общий вид (модель):
![]()
ТАУ 4.Типовые элементарные звенья и их характеристики.
Пусть система будет задана в классической форме:
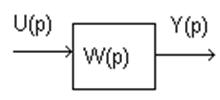
Эту систему можно расщепить на составляющие. С точки зрения математики мы будем вычислять в форме простых математических операций.
Пусть у нас:
1)
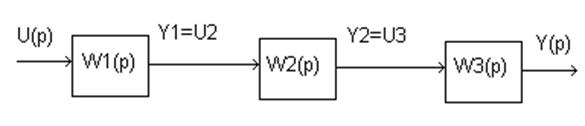
Y(p)=W(p)*U(p)
Y1(p)=W1(p)*U(p)
Y2(p)=W2(p)*U2(p)
Y(p)=W3(p)*U3(p)= W3(p)*W2(p)*U2(p)= W3(p)*W2(p)*W1(p)*U(p)
Передаточная функция:
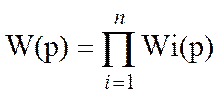
2)
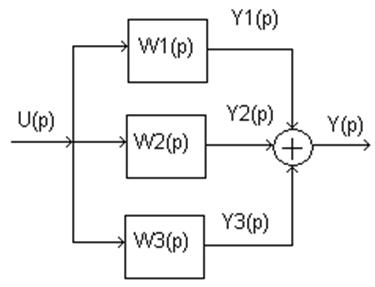
Y1(p)=W1(p)*U(p)
Y2(p)=W2(p)*U(p)
Y3(p)=W3(p)*U(p)
Y(p)=Y1(p)+Y2(p)+Y3(p)=
[W1(p)+W2(p)+W3(p)]*U(p)
Передаточная функция:
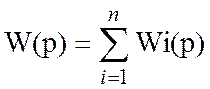
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.