Любое произвольное соединение звеньев можно представить виде 3-х типовых.
МОД 4-1. Модель идеального перемешивания
За структуру потока соответствующего модели идеального перемешивания принимается следующее: вещество, поступающее в аппарат мгновенно распределяется по всему объему V аппарата , вследствие идеального перем-я, при этом концентрация в каждой точке аппарата и на ее выходе одинакова.
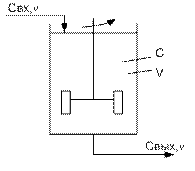
Свх,С,Свых(![]() )-концентрация вещества
)-концентрация вещества
![]()
![]() -объем
зоны идеального перемешивания
-объем
зоны идеального перемешивания
С(t)=Cвых(t)
Любой поток ![]() (моль/с) (1)
(моль/с) (1)
![]() (2)
(2)
![]() (3)
(3)
В стационарном режиме
![]()
Предположим, что в момент времени t=0
![]() , т.е. в этом случае будет происходить уже нестационарный
режим.
, т.е. в этом случае будет происходить уже нестационарный
режим.
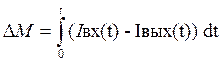 (4) →
(4) →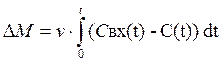 (5)
(5)
Разделим левую и правую часть на v
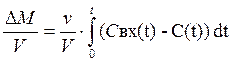 (6) →
(6) →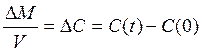 (7)
(7) 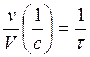 (8)
(8)
τ-время пребывания в зоне перемешивания
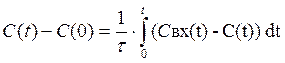 (9)
(9)
Продифференцируем левую и правую часть по времени
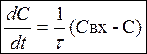 (10) – модель идеального перемешивания
(10) – модель идеального перемешивания
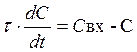 (11)
(11)
Преобразуем (11) по Лапласу при нулевых начальных условиях
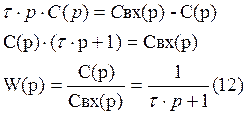
(12)-апериодическое звено 1-го порядка
Решение уравнения (10) зависит от формы входного сигнала Свх(t).
1)Cвх(t)=1(t)
![]()
ТАУ 5.Типовые статические нелинейности и их характеристики.
Можно представить либо графиком, либо функцией. Можно взять нелинейности типа:
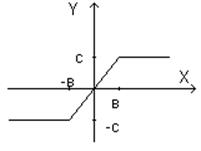 Если мы посмотрим на эту нелинейную характеристику для
X{-в; в}, то Y=K*X.
Если мы посмотрим на эту нелинейную характеристику для
X{-в; в}, то Y=K*X.
Когда: 1) Х>=в; Y=c;
2) Х<=-в; Y=-c.
Если наклон увеличивать, то будет уменьшаться расстояние в и -в. Характеристика будет приближаться к оси ординат и примет вид:
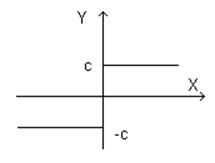 Когда: 1) Х>=0; Y=c;
Когда: 1) Х>=0; Y=c;
2) Х<=0; Y=-c.
Такого типа характеристика получила название идеальная релейная характеристика.
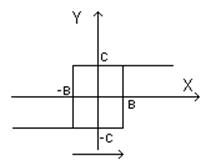 При полном приращении Х: ΔX>0
При полном приращении Х: ΔX>0
Когда: 1) Х>=в; Y=c;
2) Х<=-в; Y=-c.
![]() <0.
<0.
Реальные звенья имеют такой вид характеристики:
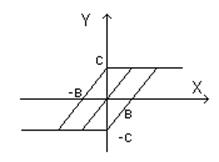
X[-в; в]; Y=K*X
![]() >0; Х>=0; Y=c
>0; Х>=0; Y=c
![]() <0; Х<=0; Y=-c
<0; Х<=0; Y=-c
X[-в;
в]; Y=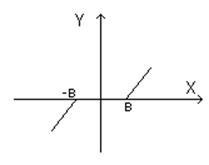 0
0
Х>в; Y=K*X
Х<-в; Y=K*X
Y=K*X
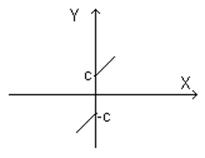 X=0: Y=-c; Y=c,
(характеристика сухого трения).
X=0: Y=-c; Y=c,
(характеристика сухого трения).
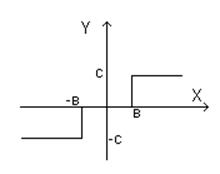
Релейное звено (трёхпозиционные регуляторы).
ТАУ 6. Преобразование структурных схем линейных непрерывных систем.
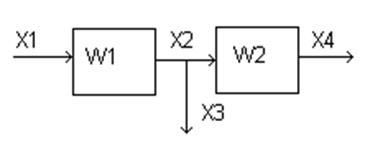
X3=X2-W1*X1
Перенесём X3 в конец:
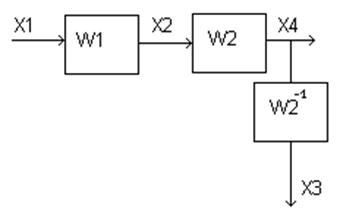
X4=X1*W1*W2
Перенесём X3 в начало:
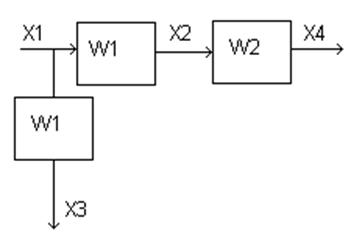
X3*W1=X4*W1*W2-X1
ТАУ 7-1. Критерии устойчивости непрерывных линейных систем.
АЛГЕБРАИЧЕСКИЕ: Критерий Гаусса.
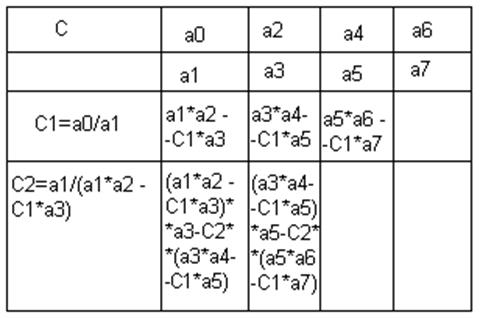 Пусть будет уравнение 7-го порядка:
Пусть будет уравнение 7-го порядка:
Анализируем знаки 1-го столбца. Если один и тот же знак у всех коэффициентов, значит, система устойчива. Это достаточно лёгкая задача.
Критерий Гурвица.
Для начало записываются две строки: в начале нечётные, затем чётные:
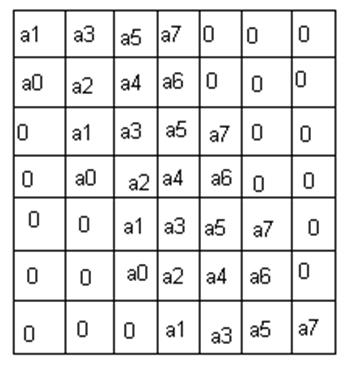 Всё это будем делать пока мы не сформируем матрицу
подходящего размера (если уравнение 7-го порядка, то последнее число будет а7).
Всё это будем делать пока мы не сформируем матрицу
подходящего размера (если уравнение 7-го порядка, то последнее число будет а7).
1) а1
2) 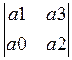
3) 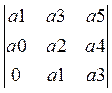
И т.д. до 7-го порядка. Находим определители, и система является устойчивой, если окажется, что все определители будут >0.
ЧАСТОТНЫЕ: Михайлова:
a0=1; p^n+a1*p^(n-1)+a2*p^(n-2)+…+an=0
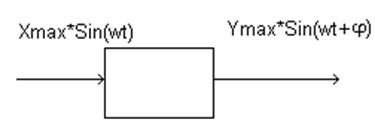 Допустим, мы имеем модель в форме д.у. движения
системы, и по этому уравнению мы записали это характеристическое уравнение.
Допустим, мы имеем модель в форме д.у. движения
системы, и по этому уравнению мы записали это характеристическое уравнение.
Формально оператор р заменяем на (јω):
(јω)^n+a1*(јω)^(n-1)+…+an=0.
Если раскрыть скобки то можем выделить:
Re(ω)+ јIm(ω)=0.
Затем можно построить: ω[0; ![]() ].
].
Пусть наша система д.у. 1-го порядка (один корень).
Возьмём корень соответствующей естественной системе: (p-p1)=0;
p1=-![]() .
.
Заменим оператор р на (јω): јω+![]() =0.
=0.
ТАУ 7-2
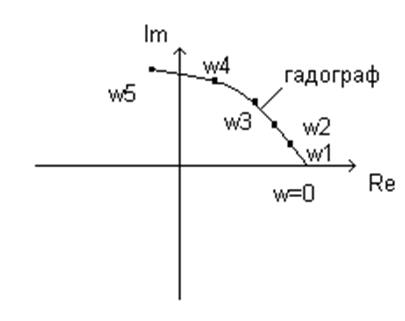
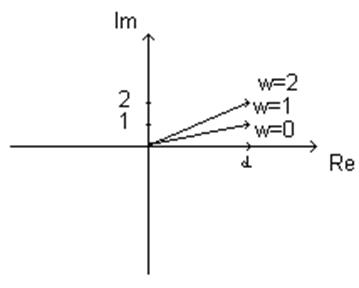
Начинаем находить точки: ω=0; ω=1; ω=2; при ω=![]() , наш вектор повернётся на
, наш вектор повернётся на 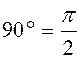 против
часовой стрелки.
против
часовой стрелки.
![]() Возьмём систему 2-го
порядка:
Возьмём систему 2-го
порядка:
(p-p1)*(p-p2)=0;
p1= -![]() 1; p2= -
1; p2= -![]() 2
2
(јω+![]() 1 )*( јω+
1 )*( јω+![]() 2 )=0.
2 )=0.
Амплитуды перемножаются, углы складываются:
A1*e^(ј*φ1(ω)); A2*e^(ј*φ2(ω))
A1*A2* e^(ј*(φ1(ω)+ φ2(ω)))
φ(ω)=n*![]() ; ω[0;
; ω[0; ![]() ].
].
Если берём комплексные числа, то правило сохраняется.
Если годограф проходит через нулевую точку, то можно сказать, что система находится на границе устойчивости.
ТАУ 8.Критерий устойчивости дискретных линейных систем.
Х(к+1)=А*Х(к)+В*U(к)
Нам надо оценить, как будет меняться Х в зависимости от того, какие будут начальные условия:
U(к)=0; Х(к+1)= А*Х(к).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.