Рассмотрим следующую систему:
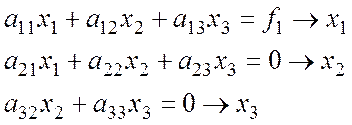
Получим реализацию на схеме а):
Возьмем систему 3-х уравнений, поменяем местами уравнения:
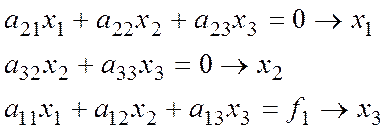
Тогда получим схему б):
ТАУ 16-2
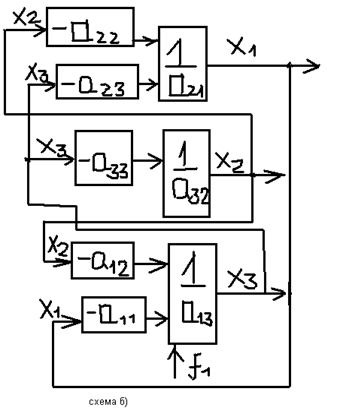Для одной и той же системы уравнений мы получили две
структуры для нахождения переменных. f1 – возмущение, которое влияет на чистоту продукта.
Оценим возможности нейтрализации воздействия (по структуре).
Схема а): любое изменение f1 приведет к изменению x1
Схема б): f1 – затянули, f1 будет проходить через блоки, будет влиять на x2, x3 пока дойдет до х1.
Если есть возможность организовать систему управления т.о., чтобы составляющая от нежелательного воздействия проходила хотя бы по 2-ум каналам до той переменной, которая для нас важна. Эти 2 канала можно организовать т.о., чтобы они могли компенсировать этот эффект (Петров) – принцип двухканальности. Если есть возможность построить систему, чтобы было два канала – есть возможность построения инвариантной системы.
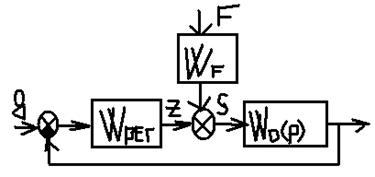Возьмем
одноконтурную систему:
g – желаемое значение Y оно не должно быть зависимо от F. Если F=сonst, система выберет отклонение Y от g за счет ОС.
Если F меняется часто, то за счет ОС длительный временной контур не успеет отработать Þ система не эффективна.
На уровне структурных решений:
1.За
счет WРЕГ Þ КУСИЛ®¥. Тогда любая ошибка будет увеличиваться до ¥, сигнал придет на Ä и будет в ¥-ое число раз >, чем от F, тогда F почти не
влияет. При большом КУСИЛ мы упираемся в условие устойчивости.
Искусственно сделаем 2-ой канал для этого возмущения.
Воспользуемся принципом 2-ухканальности Петрова. Т.к. система линейная, то мы можем по отдельности исследовать эффекты этой системы от отдельных составляющих.
Пусть g=0 и Y=0 в мом. Вр. t=0, F¹0 получим:
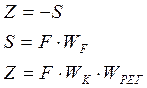
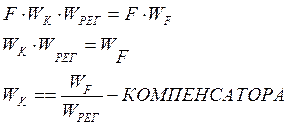
Для того, чтобы реализовать физически этот компенсатор нужно, чтобы порядок числителя был < или = порядку знаменателя. Если порядок числителя >, то физически мы не можем реализовать такой компенсатор, тогда можно разложить WK, поделив числитель на знаменатель.
ТАУ 17. Многосвязные линейные системы, их особенности.
Многосвязные системы – системы, которые имеют либо несколько входных и один выходной параметр, либо несколько входных и несколько выходных каналов, и они между собой связаны.
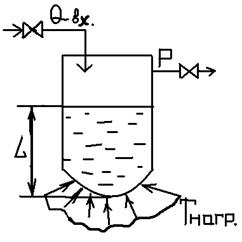Рассмотрим
на примере парового котла:
L – уровень; Т – температура; Р – давление. Исходя из количества тепла можно определить ТНАГР.. Если эта Т=const, LЖ, т.е. mЖ=const, то будет формироваться постоянное количество пара. Предположим оно регулярно забирается потребителем.
Пусть
приток воды оказался меньшим, чем нужно уровню, возрастает количество пара. Это
изменение расхода сказывается на давлении пара. Если температура увеличитсяÞиспарение больше, уровень меньше при Q=const.
На уровне такого технологического объекта мы установили, что хотя входных и
выходных сигналов по два, контуров здесь получается больше(4 контура). Каждый
входной канал формирует 2 воздействия.
Сформируем вектор входных воздействий:
W(p) – матричная передаточная функция.
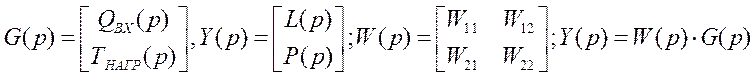Важная отличительная черта от
одноконтурных систем – оценка степени взаимного влияния одних каналов на
другие.
Рассмотрим
вариант, когда в матричной форме в виде матричных передаточных функций есть
последняя цепочка системы:
(перемножать именно в такой
последовательности)
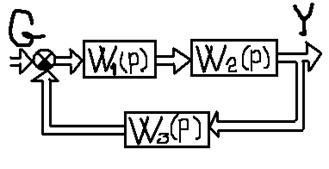
Для параллельного соединения:
В матричной форме 
ТАУ 17. Многосвязные линейные системы, их особенности.
Многосвязные системы – системы, которые имеют либо несколько входных и один выходной параметр, либо несколько входных и несколько выходных каналов, и они между собой связаны.
Рассмотрим
на примере парового котла:
L – уровень; Т – температура; Р – давление. Исходя из количества тепла можно определить ТНАГР.. Если эта Т=const, LЖ, т.е. mЖ=const, то будет формироваться постоянное количество пара. Предположим оно регулярно забирается потребителем.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.