Ответы на экзаменационные билеты № 1-30 дисциплины "Адаптивные системы управления" (Математическое описание сигналов и операторов в непрерывных линейных детерминированных системах. Адаптивные системы управления), страница 8

Пусть приток воды оказался меньшим, чем нужно уровню, возрастает количество пара. Это изменение расхода сказывается на давлении пара. Если температура увеличитсяÞиспарение больше, уровень меньше при Q=const. На уровне такого технологического объекта мы установили, что хотя входных и выходных сигналов по два, контуров здесь получается больше(4 контура). Каждый входной канал формирует 2 воздействия.

Сформируем вектор входных воздействий:

W(p) – матричная передаточная функция.

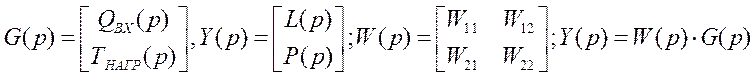          Важная отличительная черта от одноконтурных систем – оценка степени взаимного влияния одних каналов на другие.

Рассмотрим вариант, когда в матричной форме в виде матричных передаточных функций есть последняя цепочка системы:

 (перемножать именно в такой последовательности)

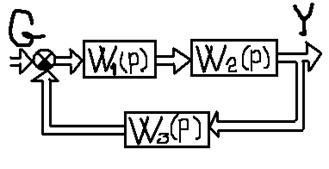
Для параллельного соединения:

В матричной форме

ТАУ 18-1. Синтез многосвязных линейных систем с использованием модального управления, компенсаторов.

1. На основе модального управления. Предполагаем что наш объект представлен в области переменных состояния и для каждой из переменных состояния задаются динамика переходного процесса из условия апериодического характера этого переходного процесса. Задаемся характером перехода (если брать свободное движение и считать, что ДУ 1-го пор-ка (1 корень) ) значение которого можно определить.

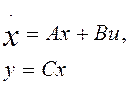
Рассмотрим скалярную систему.

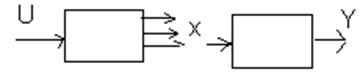
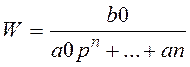, если в числителе не присутствует оператор р а только некоторый коэффициент то у=х1; . Если матрица А будет иметь форму, 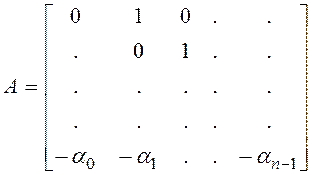 , то расчеты делать просто, а если А имеет другую форму необходимо сделать преобразования чтобы свести матрицу А к предыдущему виду . Перейдем к новому вектору х с помощью преобразований 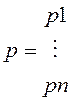  для его нахождения воспользуемся след. правилом

Произвольная матрица А

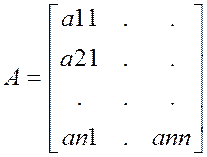, где матр.  

Для определения р воспользуемся след схемой:

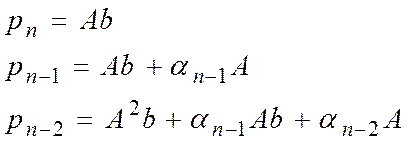
- собственные числа матрицы А. Сначала найдем  затем р сделаем преобразования матрицы.

Закон управления при модальном управлении и структура регулятора задается

U=g-kx

ТАУ 18-2

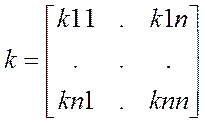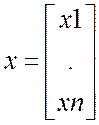,   если в нашу модель подставить управляющее воздействие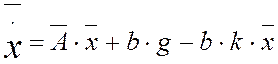  

В однородном виде 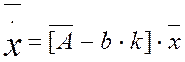 на основании этого уравнения можно получить решение x. В  результате операции поменяются коэффициенты , что приведет к изменению характера, корней, а следовательно к изменению переходного процесса.

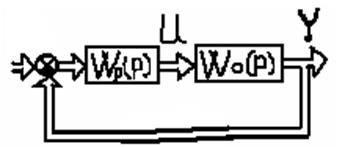2. С использованием компенсаторов

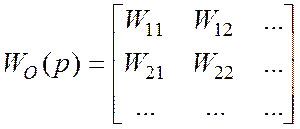, аналогично W_РЕГ(p) – передаточная матрица. Пусть наша система будет развязана по выходам от управляющих воздействий. Такое управление получило название – автономное управление (для одного канала – одно управление). Задача: чтобы система была развязанность по каналам. Если бы (1),тогда мы бы регулятор взяли бы аналогичный: (2). Если

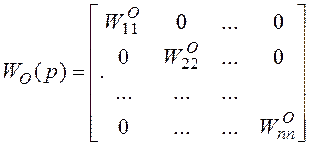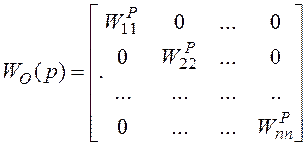(1)        (2)

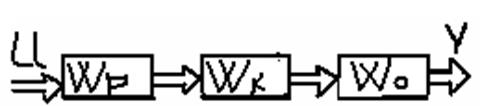
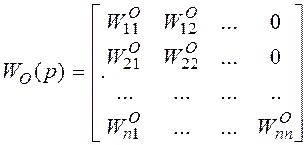, в этом случае, чтобы получить систему, которую можно было бы отнести к классу автономных многосвязных систем сделаем структурное преобразование схемы. Внесем в структуру компенсатор:

потребуем, чтобы W_O(p)W_K(p) обладало свойсвом:

W_O(p)W_K(p)=diagW_O(p) или

W_K(p)= W_O^-1 diagW_O(p).

Задаемся y_жел, m_жел, делаем расчеты, проверяем насколько W_K(p)= W_O^-1 diagW_O(p) – этот компенсатор является физически реализуемым.

ТАУ 18-3

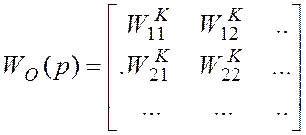, где 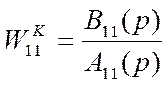 - дробно-рациональные функции, порядок числителя < порядка знаменателя Þ физическая реализуемость. Если компенсатор нельзя физически реализовать, то используют частичную компенсацию (в статике) 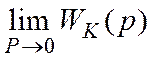 - получаем статический компенсатор, жесткий коэффициент усиления.

Вставим дополнительный блок на уровне задающего сигнала. Развязать каналы Þ уменьшить число регуляторов.

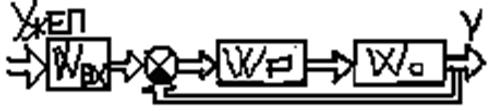
Чаще пользуются:

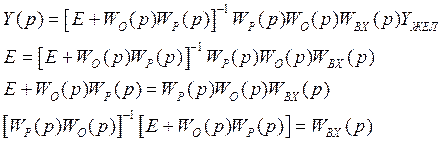
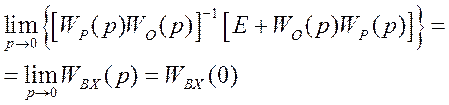
ТАУ 19. Методы фазовой траектории при исследовании нелинейных систем.

Допустим нелинейная система описывается 2-мя ДУ:

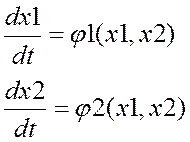,              нелинейные ф-ции.

Избавимся от одной из переменных.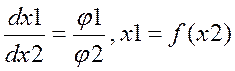 можно построить график:

М0-начальная точка

Такие графики получили название фазовых портретов

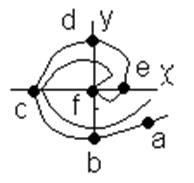Данная линия будет характеризовать фазовую траекторию движения системы. Если поменять н.у. то будет другая характеристика. Если собрать множество траекторий при разных н.у. то множество этих линий создадут фазовый портрет. Эти фазовые портреты будут существенно меняться от состояния системы(устойчива, неустойчива). Т.к. лин. система явл. частным случаем нелинейных то мы можем перейти к анализу нелинейных систем на основе линейных. Рассмотрим лин систему 2-го порядка, задающее воздействие =0.