Другие предметы \ Теория автоматического управления

Ответы на экзаменационные билеты № 1-30 дисциплины "Адаптивные системы управления" (Математическое описание сигналов и операторов в непрерывных линейных детерминированных системах. Адаптивные системы управления), страница 10

Pm=Y(m)-Y(m-1)=1-Y(m-1)       Qm=U(m)-U(m-1)

                                      

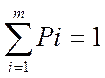
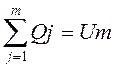
Мы можем найти передаточную ф-цию нашего объекта:

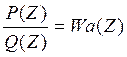 c другой стороны нам дана передаточная ф-ция объекта:

 

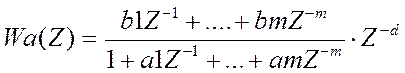
Разделим все коэффициенты на Q0 и получим

           

   

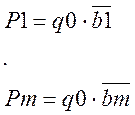
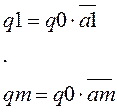
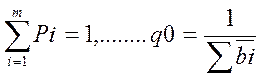
Вернемся к нашей передаточной ф-ции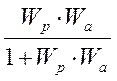 Wзс=     WзсP(Z)

 

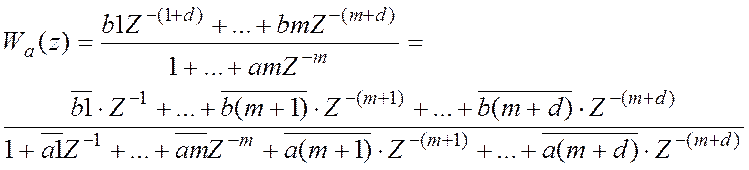
P(Z)= 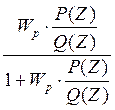 неизвестная Wp

P(Z)+P(Z)W(p)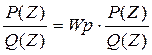      à    P(Z)=Wp*()

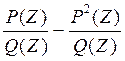1=Wp*() Wp=получили передаточную ф-цию регулятора


ТАУ 22. Синтез дискретных компенсационных регуляторов из условия желаемого расположения полюсов ХАУ.

Пусть структура системы имеет вид: x(k+1)=Ax(k)+Bu(k). Пусть структура регулятора будет в такой же матричной форме: u(k)=-Gx(k). Неизвестной является матрица G. Воспользуемся косвенными показателями качества, например расположением полюсов (корней ХАУ) системы.

Пусть полюса ХАУ z1, z2,…, zi известны.

x(k+1)=Ax(k)-BGx(k);   zx(z)=Ax(z)+Bu(z);        [zI-A]x(z)=Bu(z);  (zI-A+BG)x(z)=0;

Для разомкнутой функции можно сказать, что х связан с коэффициентом: -G[zI-A]-1B=Tp;

Когда система замкнута, то можно записать: -G[zI-A+BG]B=Tз;        

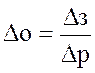I-Tp=To;

 (zI-A+BG)=(zI-A)(I+[zI-A]-1B)

Если взять модуль, то 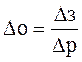 справедливо. Тогда получим, что To=I+G[zI-A]-1B= ;  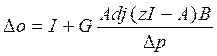 . Необходимо, чтобы . Это также является качеством системы. Можно записать, что: K=Adj(zI-A)B; 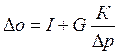 . K=[K1,K2,…Ki];

. Когда можно найти К-1, то имеем решение задачи: .

[B AB A2B …], когда система управляема, то можно найти элементы матрицы G. В случае кратности корней, продифференцируем выражение :

z2:;     ;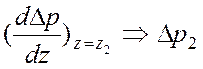

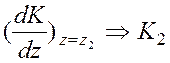z3:;        ;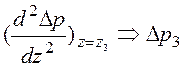

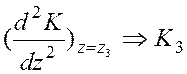Все это проделано при условии одноканального управляющего воздействия.


ТАУ 23-1. Синтез дискретного регулятора из условия минимизации дисперсии выходного сигнала

Объект линейный, без запаздывания, записанный в виде передаточной функции.

 


                             

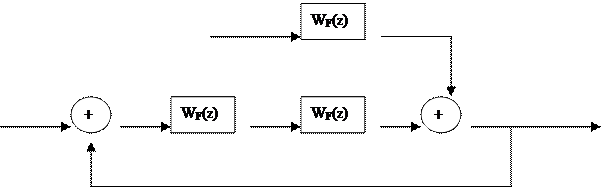g                     y                    u                                          y                    

--    

Чтобы регулятор уменьшал воздействие , принимаем входной сигнал равным нулю, используя то, что эта система линейна.  можно математически представить как результат прохождения какого-либо шума (белого) через фильтр. Привяжемся к характеристикам белого шума: M{V(R)}=0;

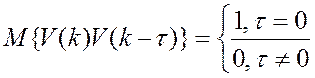. На основе фильтра можно получить необходимый сигнал . Зададимся формой W:

     

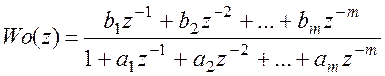
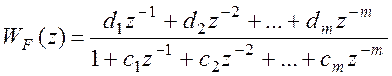
В области Z-преобразований можно записать связь сигнала на выходе системы, регулятора, фильтра и т.д. Обозначим критерий, с помощью которого будем оценивать систему Y нормированный – математическое ожидание. y=yфактич-my. Имеем в виду, что объект инерционный.

Пусть будет: 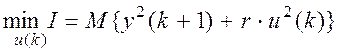, r - весовой коэффициент соответствия между y2(k+1) и u2(k).

На основе этого условия необходимо синтезировать систему. Когда есть функция и необходимо найти экстремум, то необходимо взять производную по этой переменной и приравнять ее к нулю. Методика основана на этом условии. Запишем сигнал относительно выхода: 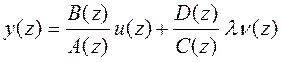, умножим на z: 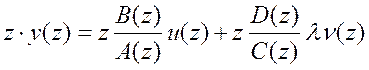;  (1)

Ограничимся только первыми составляющими (a, b, c, d).

;

;

;

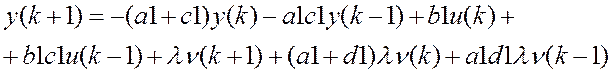Имеем составляющую для критерия:


ТАУ 23-2

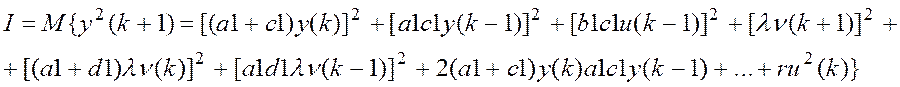
. От данного выражения берем производную по u(k).

;

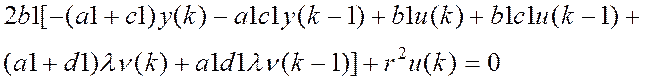                (2)

Избавимся от белого шума. Выразим  из (1) и подставим в (2).


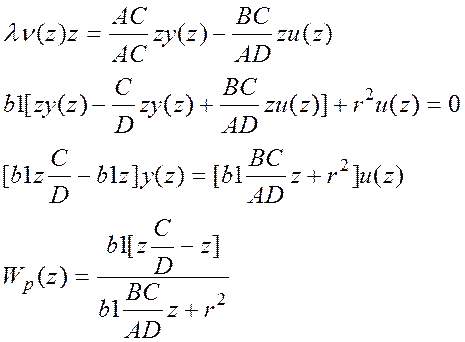
ТАУ 24. Элементы вариационного исчисления и применение их для расчета оптимального управления.

Сформируем математический критерий, с помощью которого будем оценивать систему. Функции, входящие в состав критерия имеют гладкий характер. Чем больше можно продифференцировать функцию, тем она глаже.

Задача Лагранжа.

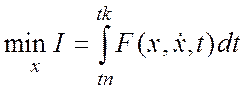 или можно рассматривать .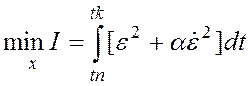

Найти аналитическую форму х, которая обеспечит критерий. Ограничимся данной задачей.

Пусть имеем решение оптимального движения системы:

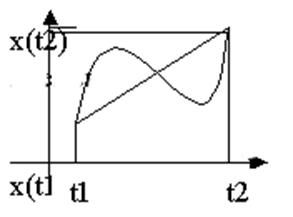Есть вариация ;  - функция, которая в момент времени ;        - вариация. 

Такую неоптимальную функцию заводим под интеграл в данный критерий.

. Так как речь идет об экстремуме, можно продифференцировать по базовым составляющим и, используя разложение в ряд Тейлора, можем выделить базовые значения. 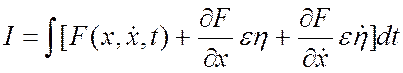.  Когда можно найти разницу между критерием, который включает оптимальную функцию, и полученным критерием, то можно сказать о нахождении вариации.

Скачать файл