Ответы на экзаменационные билеты № 1-30 дисциплины "Адаптивные системы управления" (Математическое описание сигналов и операторов в непрерывных линейных детерминированных системах. Адаптивные системы управления), страница 6

ТАУ 13-2

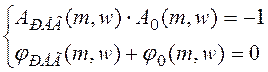        - больше неизвестных, чем число уравнений.

КПР
ТИ
КПР/ТИ

Мы можем определить все частоты: будем задаваться значениями [w_min, w_max] с шагом Dw – и получить для различных w решение этих 2^х уравнений. Далее составляем таблицу:

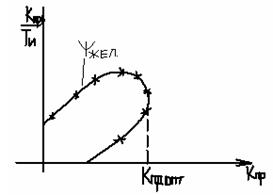Строим график:

Чем > К_ПР, тем лучше.

Если взять ПИД-регулятор вида: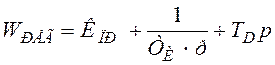                                              

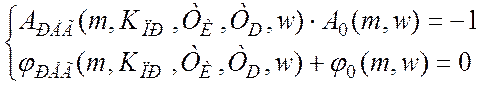
Подобрали, что неплохие результаты получаются при Т_D=0,1…0,15Т_И. Пусть Т_D=0,15Т_ИÞподставим в W_РЕГ и дальше та же методика (табл.,график), учитывая, что корни близко к Im.

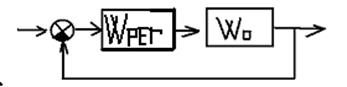ТАУ 14-1. Синтез систем управления методом расчета параметров регулятора на желаемый показатель колебательности.

ПИ-регулятор: Задаемся W_РЕГ. j=arcSin(1/M_ЖЕЛ). Имеем систему вида:

Передаточная ПИ-регулятора имеет вид:.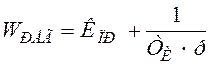

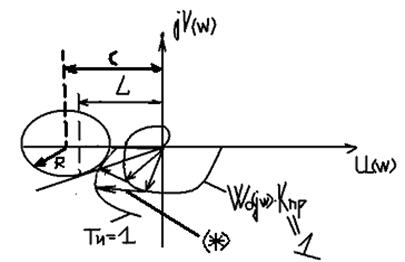Строим АФЧХ, при К_ПР=1 для построения интегральной составляющей:

Здесь окружность строится:

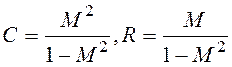
Где L=1/K_{ПР.РАСЧ.}. Зададимся численными значениями Т_И=1;5;10;100;…

Строим один график для К_ПР=1, Т_И=5 и т.д.Þполучим семейство кривых, причем

1/Т_Иjw=-j(1/ Т_Иw).

Знак минус означает поворот по часовой стрелке(*). Задаемся частотами w [w₁, w₂, …w_n], находим 1/ Т_Иw_i. Получим новую кривую, проводим окружностьÞполучаем LÞ K_{ПР.РАСЧ}=1/ L. Составляем таблицу:

ТИ	1	5	10	100
KПР.РАСЧ

Строим график

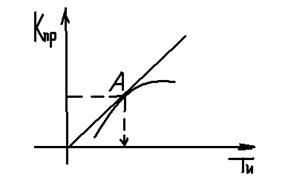
Точка А является лучшим вариантом.

Передаточная ПИД-регулятора вида: .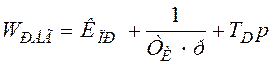

Зададим:

ТИ	1	5	10	100
ТD	0,5	5	6	20

Строим АФЧХ, при К_ПР=1, интегральная составляющая –j(1/Т_Иw_i), дифференциальная составляющая jТ_Dw_i. Тогда в силу –j(1/Т_Иw_i)+ jТ_Dw_i при построении вектор –j(1/Т_Иw_i) поворачиваем по часовой на 90⁰ и jТ_Dw_i на 90⁰ против часовой стрелки, получим суммарный вектор j(-1/Т_Иw_i+Т_Dw_i):

ТАУ 14-2

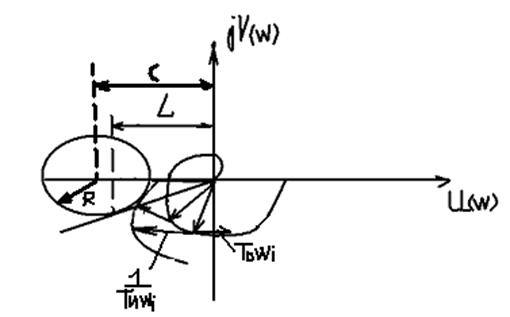
, где окружность строится: .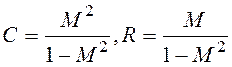

Составляем таблицу:

ТИ	1	5	10	100
ТD	0,5	5	6	20
КПР.РАСЧ.

Т.о. мы можем выполнить расчет параметров настройки регулятра.

ТАУ 15-1. Синтез системы управления с использованием упредителей Смита.

Пусть объект содержит большое запаздывание. На систему действует возмущающее воздействие F. Передаточная объекта:

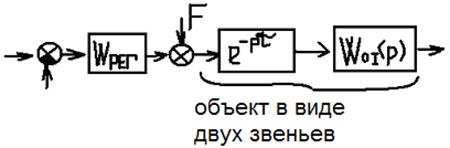
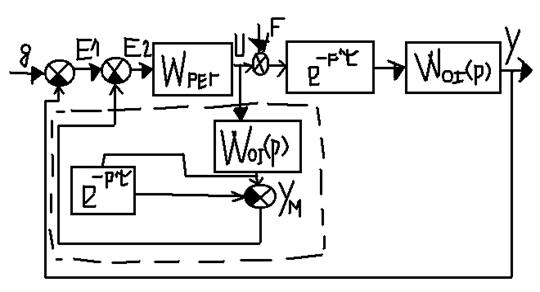Сложность – в запаздывании, решение этой задачи предложил Смит:

Упредитель Смита – пунктиром.

Имея эту структурную схему, можем попробовать записать связь выхода системы с задающим воздействием и возмущающим.

,                  

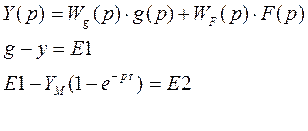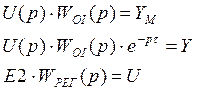
F=0, , ,

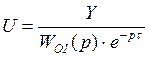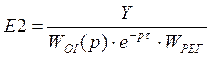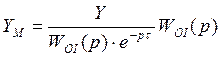
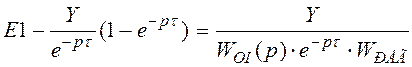
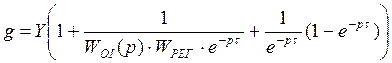
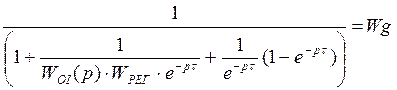
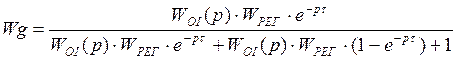
В области тех частот, которые характерны для работы системы, выполняется условие: пусть Þ пренебрегаем единицей:

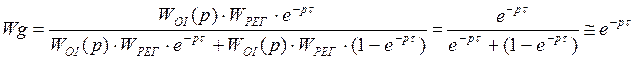
ТАУ 15-2

, получаем вид W – чистое запаздывание, от него мы не можем избавиться у реального объекта.

Возьмем задающее воздействие нулевое: F¹0, g=0:

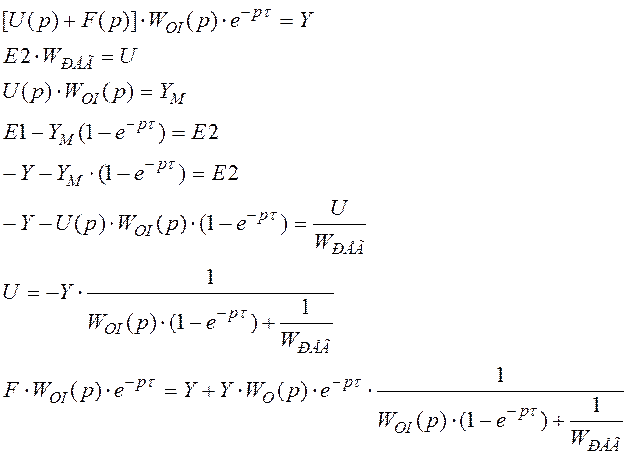
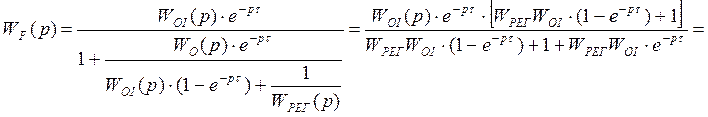
(W_РЕГW_OI>>1)

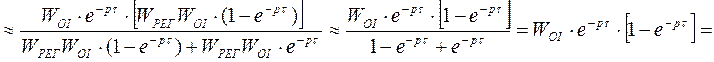
ТАУ 16-1. Синтез инвариантных систем управления

Инвариантные системы – это достаточно важный класс систем. В пространстве часто меняется нагрузка, что изменяет технологические параметры аппарата и вызывает необходимость коррекции потоков. Теория инвариантных систем практически создана 40 лет назад. Система описывается уравнениями:

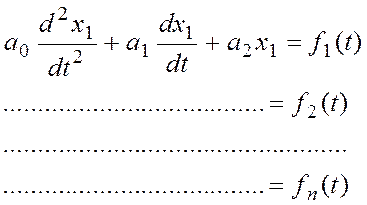Если решение нечувствительно к воздействию составляющей правой части, то система может называться полностью инвариантной.

Если влияние воздействия малое (<e), то считается, что система инвариантна к f₁ до этого значения e.

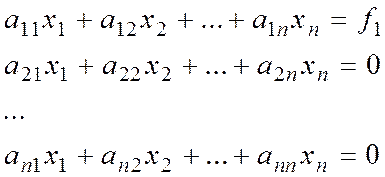
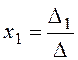 заменим столбец x₁ на .

Т.е.

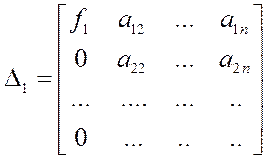 Можно сказать, что решение x₁:             .

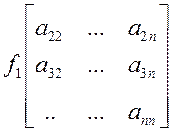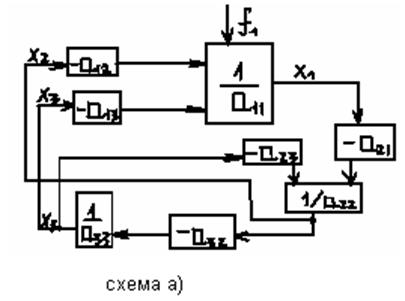Если f₁¹0, то для того, чтобы это решение x₁ не зависело от f₁ÞD₁=0. Если есть модель системы управления, которую можно свести к такой форме (алгебраической), то можно найти каким соотношениям должны удовлетворять коэффициенты, чтобы один из сигналов x был не зависим от возмущений.