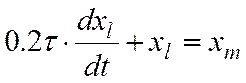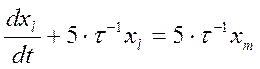
; 
Все звенья будут одинаковые и иметь это ур-ние, но будут отличаться только индексами.
Когда будем переходить от матричной формы записи модели к скалярной, получим систему ур-ний :
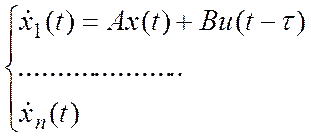Обозначим
u(t-τ) = xn+1
;
;……..;
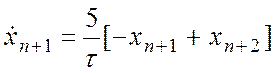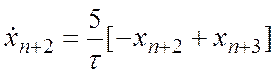ТАУ 27-4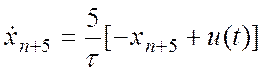
/это и выше – писать в столбик/
С учетом этих 5-ти дополнительных ур-ний можно сказать, что получили систему без запаздывания, но большего порядка.
Изменяются матрицы A и B → 
и 
и дальше находим Uопт.
5. Для линейных непрерывных нестационарных объектов.
Рассмотрим нестационарный объект, у которого с течением времени изменяются элементы матриц А и В.
= A(t)x+B(t)u
J=∫ [XTDX + UTC-1U]dt
Зададимся ф-цией φ = min J ; φ = XTR(t)X
Запишем ур-ние Белмана:
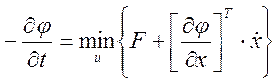
–XT·
(t)·X=min{
XTDX+UTC-1U+XTR(t)[A(t)X+B(t)U]+[
A(t)X+B(t)U ]TR(t)X }
–XT·(t)·X=min{XTDX+UTC-1U+XTR(t)A(t)X+XTR(t)B(t)U+XTAT(t)R(t)X+
+UTBT(t) R(t)X }
Дальше берем производную от {•}: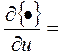
C-1U+ C-1U+BT(t)R(t)X+ BT(t)R(t)X = 0
Uопт = - CBT(t)R(t)X ; UTопт = - XTR(t)B(t)C.
Подставляем Uопт в функц-ое ур-ние :
–XT·(t)·X=XTDX+XTR(t)B(t)CBT(t)R(t)X+XTR(t)A(t)X–XTR(t)B(t)CBT(t)R(t)X+ +XTAT(t)R(t)X–XTR(t)B(t)CBT(t)R(t)X
Дальше сократим на XT и X : –(t) = D+ R(t)A(t) –R(t)B(t)CBT(t)R(t)+ AT(t)R(t)
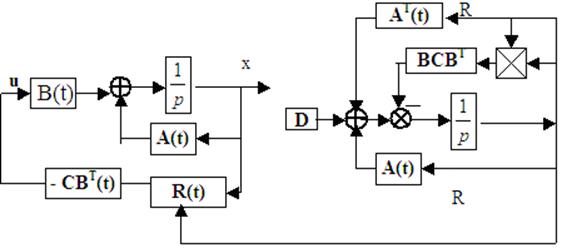
Получили традиционное ур-ние Реккати. Нелинейное. Нарисуем структуру системы:
Введем критерий Красовского:
J=∫[XTDX+XTR(t)B(t)CBT(t)R(t)X+UTC-1U]dt
Поскольку дополнит. составляющая не содержит U, тогда Uопт остается неизменным.
При нахождении матрицы R(t) дополнит. Составляющая сократиться:
–
(t) = D+ R(t)A(t) + AT(t)R(t)
Получили линейное ДУ
ТАУ 28-1. АКР для линейных дискретных систем.
Пусть объект будет стационарный: x[(k+1)T] = Ax(kT)+Bu(kT)
Эл-ты матриц А и В постоянные.Х – это отклонение от базовых значений.
Разговор идет об стабилизации системы.
J=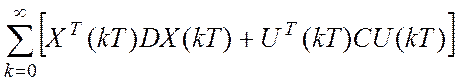
Поскольку Х – отклонение, то поставим задачу минимизации, т.е. чтоб отклонение было наименьшим.
Введем ф-цию φ(х(kT)) = minJ . Пусть φ(х(kT)) = ХТ(кТ)RX(kT)
T и dt – разные значения.
Для дискретн. системы, при условии, что Т очень маленькое (напр. 0.001*tрег) тогда можно пользоваться методами расчета для непрерывных систем. Но Т большое, поэтому ур-ние Белмана не подходит. Можно записать рекурентное ур-ние, которое будет описывать эффективность работы системы.
Пусть стратегию управления наилучшую подобрали для тактов, начиная со 2-го такта. Не успели найти оптимальное управление на 1-ом такте. Найдем это для 1-го такта:
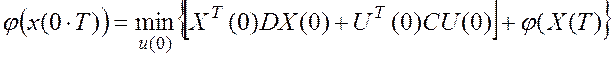
где 
-
решение для всех остальных тактов.
Остается найти решение для 1-го такта. Т.к. А,В,С,D = const , тогда можно сказать , что решение для 1-го такта будет справ-во и для остальных тактов.
Функцию
можно
рассмотреть как 
ΔХ = Х(Т) – Х(0)
Разложим
ф-цию в ряд Тейлора: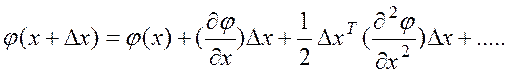 
Т.к. Т будет значительное, тогда Δх будет значительное и поэтому используем и квадратичный член ряда, а остальные будут незначительные. Подставляя, получим:
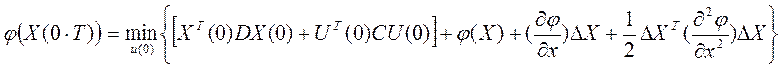Т.к. в составе 
в явном виде нету U(0),
тогда их можно вынести за скобки и перенести в левый бок и сократить:
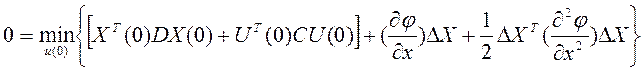
Дальше подставим ΔХ и возьмем производную:
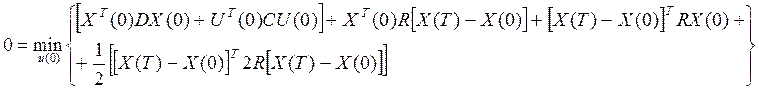
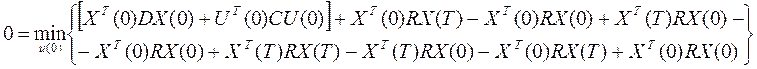
ТАУ 28-2
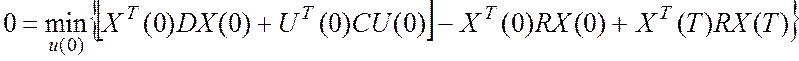
Дальше вместо Х(Т) подставим АХ(0)+ВU(0):
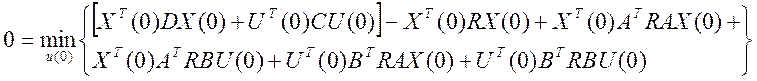Продифференцируем по U(0): 
;
Чтобы найти матрицу R, нужно Uопт(0) подставить в функц-ное ур-ние:
Для этого введем обозначения: Uопт(0) = M·X(0)
Uопт(kT) = M·X(kT)
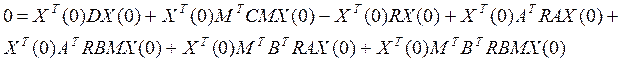
Сократим на ХТ(0) и Х(0):
Получили тяжелое для решения алгебраическое ур-ние.
ТАУ 29-1. Синтез наблюдателей переменных состояния.
Рассмотрим объект, который имеет линейную модель:
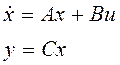
Пусть все переменные состояния не доступны измерению. На основе модели матрицы А,В,С – известны. Структура объекта:
uxy
Составляющие u и y – известны.
Дальше будем строить наблюдатель, в который будем вводить те переменные, которые доступны измерению.
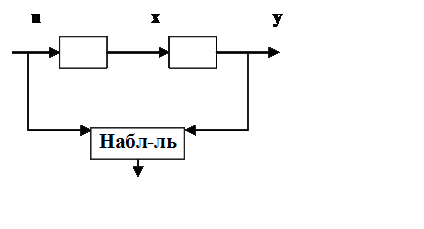Ошибка : x - 
= e. С
течением времени нужно, чтобы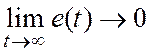 
Нужно чтобы время измерялось каким-нибудь периодом, который был бы приближен к времени переходного процесса (t→T соотв. tрег или был меньше). На сегодняшний день этот Т должен быть в 2-4 раза меньше tрег.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.