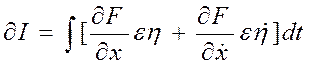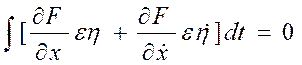Ответы на экзаменационные билеты № 1-30 дисциплины "Адаптивные системы управления" (Математическое описание сигналов и операторов в непрерывных линейных детерминированных системах. Адаптивные системы управления), страница 11

;      ; Сведем к данное выражение: .

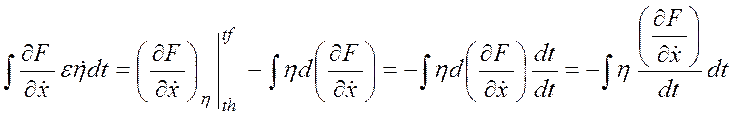Тогда можем получить следующее выражение:

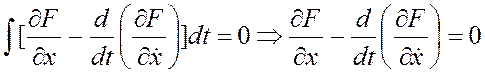. Уравнение Эйлера-Лагранжа. Рассмотрим пример: Пусть 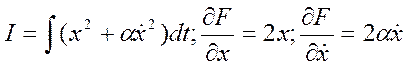. Имеем дифференциальное уравнение и его решение находим в виде: 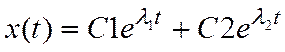. Для устойчивой системы необходимо иметь такие условия, чтобы С1=0, тогда: 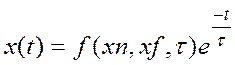. Это соответствует апериодике первого порядка. Когда объект описывается апериодическим объектом первого порядка, то для этой системы необходимо рассчитывать П – регулятор.

ТАУ 25-1. Вывод основных соотношений принципа максимума. Проблемы его исследования.

Принцип максимума Понтрягина.

Постановка задачи. Существует критерий и модель движения объекта (в данном случае линейная)

; Обозначим критерий какой-либо переменной, например , продифференцируем данное уравнение, тогда: 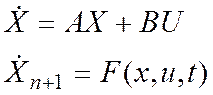. Если F(..)=1, то тогда правая часть дополнительной составляющей не меняется и она не влияет на классический метод решения и можно проигнорировать  и получаем решение без дополнительной составляющей. Основные формулы принципа максимума на основе задачи о быстродействии. . Для этой системы необходимо найти управляющее воздействие. Пусть известна траектория движения.

ПустьU на некоторое время сделает скачок, а после вернется к своему состоянию. Тогда можно сказать, что сдвиг по U  происходит на . Движение будет отличаться от Х. Х* - неоптимальное движение. Задача. Найти траекторию Х*, динамику вариационного движения системы. . Рассмотрим узкий интервал: имеем 3 точки: общая для Х и Х*; оптимальная точка; точка неоптимальной траектории. Учитывая, что - мала, то можно брать точку на оптимальной кривой и находить следующую точку, используя уравнение прямой. Для неоптимальной траектории:.

Для оптимальной: .

Найдем разность:

Берем интервал . . С другой стороны: , продифференцируем, подставим в левую часть, получим: .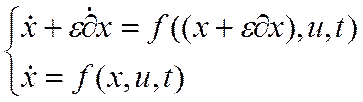

ТАУ 25-2

Раскладываем в ряд Тейлора и ищем разность между оптимальной и неоптимальной траекториями:

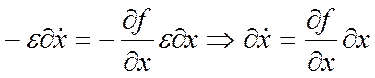. Возьмем t = tf. Через конечный пункт проводится плоскость (в данном случае прямая). Эта плоскость отделяет неоптимальные точки от оптимальных. Место плоскости можно охарактеризовать нормалью . Проведем касательную к неоптимальной траектории в момент времени tf. Если рассматреть скалярное произведение двух векторов, при условии, что угол между ними тупой, то: ; Вводим функцию Гамильтона: , тогда: . Когда неоптимальная траектория станет оптимальной, то неравенство станет равенством. Когда можно найти управляющее воздействие, которое обеспечит максимум левой части, то будет возможность заменить неравенство равенством.

ТАУ 26-1. Динамическое программирование. Рекуррентное уравнение. Уравнение оптимальности. Проблемы исследования.

Пусть было х денег, у средств пошло на клуб, х-у на компьютер. Суммарный доход составил gy+h(x-y). Необходимо максимизировать доход. Задача оптимизации. Работаем год, потом всё продаём  a(у), полученные деньги b(х-у). Получили х₁ денег, а доход V1 распределили между собой. снова пустили в оборот. До продажи имели задачу: 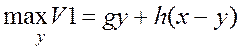. После получения прибыли . Однако задачу можно поставить сложнее. Разработаем стратегию на 2 года (прибыль за два года).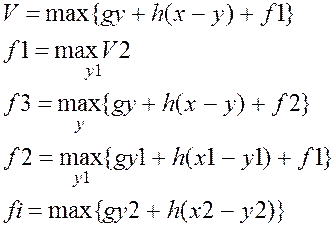

 Исходя из вычислений, получаем рекуррентное уравнение: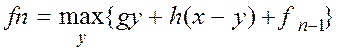 

Вывод уравнения оптимальности.

Какая бы ни была стратегия управления на предыдущих этапах, начиная с некоторого этапа, для остальных можно найти оптимальную систему управления. Исходя из этого, рассмотрим непрерывный вариант динамической системы.

Найдем экстремум. Допустим мы управляли следующим образом: обозначим .

, с момента  данный критерий принимает экстремальному значению. Разложим данное уравнение в ряд Тейлора:

.

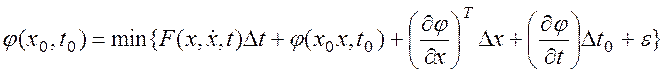Когда  и  малы, то занулим все составляющие. Тогда получим: 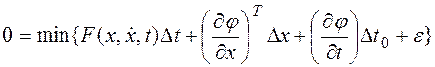 . Выразим  через  .

ТАУ 26-2

Исходя из этого имеем: 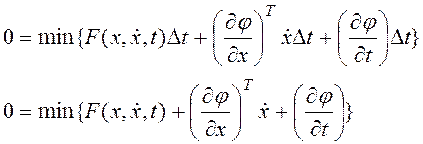. Экстремум обеспечим за счет   или . . 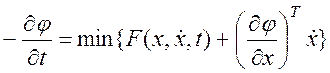Получаем уравнение для нахождения оптимального закона управления, исходя из того, что  явно не содержит ни , ни .

ТАУ 27-1. Аналитическое конструирование регуляторов для линейных непрерывных систем