Ответы на экзаменационные билеты № 1-30 дисциплины "Адаптивные системы управления" (Математическое описание сигналов и операторов в непрерывных линейных детерминированных системах. Адаптивные системы управления), страница 14

Дальше, когда переменные состояния     будут формир-ся  и будут близкие к  х, тогда можно сформировать закон управления, построить регулятор.

                         

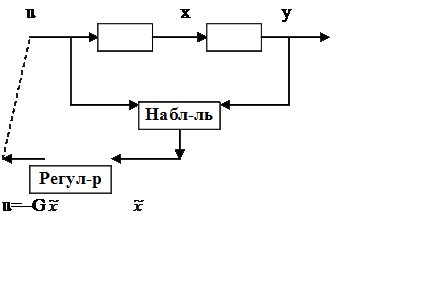
Этот наблюдатель нужен для использования  для достижения желаемых значений.

Нахождение законов для реализации наблюдателя:

Когда А и В известны, тогда набл-ль можно реализовать в следующей форме:

Отсюда будем находить . Для этого нужно решить систему ДУ, но нужно иметь начальные условия. Если бы эти условия были равны условиям объекта  (0) = х(0) , то решение получили бы такое же как и для объекта.

Т.к. переменные состояния неизвестны, то (0) – неизвестны. Нужно подбирать их самостоятельно или найти какое-нибудь правило. Дальше нужно ввести параметры для оценки , которые получим на основе наблюдателя.

Воспользуемся еще одной формой записи : y = Cx, тогда .

     когда эта разница →0, то  будут близкие к х.

Введем    и заменим   другим вариантом:

В правой части появляется дополнит. составляющая, которая вносит коррекцию.

ТАУ 29-2 Такой наблюдатель предложил Люснбергер.  - вносит дополнит. стабилизацию в систему, за счет которой  будет ближе к х.

                  

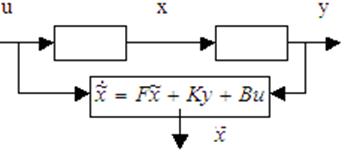
В состав матрицы F входит переменная К:

F = А – КС , где К – матрица, элементы которой являются коэф-ми усиления.

Это ур-ние можно рассмотреть с точки зрения устойчивости. Можно рассмотреть однородное ур-ние: 

 - характеристическое ур-ние.

Его можно записать в виде: 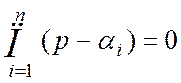   ,где α_i – корни характ-го ур-ния.

Дальше можно задаться этими корнями, один или два ближе к оси Im (α₁). Ближний корень будет дольше тянуть хвост переходного процесса. Выбрав t_рег, можно найти α₁ (t_рег ~3…4 α₁). Остальные корни можно взять на порядок больше, чтобы быстрее закончился переходной процесс.

Дальше можно раскрыть скобки, получить характеристическое ур-ние, найти составляющие γ_1, γ₂ … методом сравнения коэф-тов при p^n-1, p^n-2,….. Затем можно вернуться к элементам матрицы F и элементам матрицы К.

Рассмотрим другой вариант.

Можно найти W(объекта) и W(наблюдателя) и попробовать их приравнять:

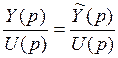 при нулевых условиях Х(0).

Т.о. мы от переменных состояния будем стремиться избавиться.

               

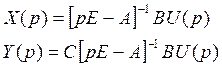
На основе модели наблюдателя при нулевых начальных условиях:

   вместо Y подставим Y = CХ:

 

, тогда

Дальше приравняем W_об и :

ТАУ 30-1. Адаптивные системы управления. Классификация. Синтез адаптивной системы с эталонной моделью на основе подстройки коэффициентов уравнения в переменных состояния.

Адаптивные – системы, способные приспосабливаться к объектам. Способны изменять свою структуру, коэф-ты настройки регуляторов с целью обеспечения хороших показателей качества. Система приспосабливается к пар-рам внешней среды, которые изменяются с течением времени. Бывают:

1) C идентификацией параметров модели объекта управления

2) C эталонной моделью на основе подстройки коэффициентов уравнения в переменных состояния

 

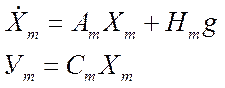
Модель эталонной системы

Параметры А,Н,В,С- неизвестны, известен только порядок матриц.

Нужно подобрать регулятор т.о. чтобы с течением времени адаптации он изменил свои параметры так , чтобы вместе с обьектом управления он создал такой же выход как и эталонная модель. Нужно взять  - ошибка  .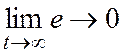

Возьмем упрощенный вариант системы: x=Ax+Hg+U, U-выход регулятора

 (напоминает П-рег-р)   Адаптация будет идти на основе параметров регулятора    найдем ур-ие для ошибки

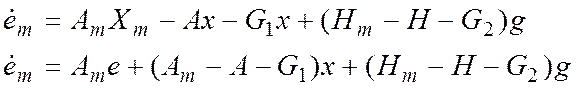 поскольку x,g, доступны измерению, то они известны   будем привязываться к функции Ляпунова чтобы оценить устойчивость

Матрицы R, должны быть позитивно определены чтобы была уст-ть   ,   Q- положительна продифференцируем исходную ф-цию по переменным

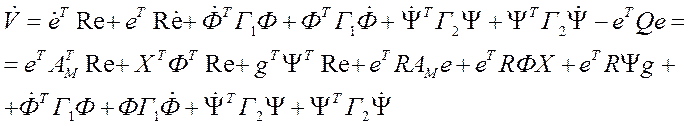
ТАУ 30-2

   

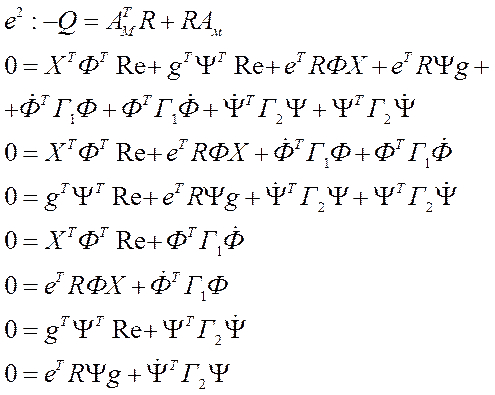
Можем сократить на

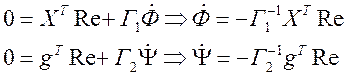(1)

Если проинтегрируем уравнения (1) ,то мы получим значения элементов Ф и  в любой момент времени 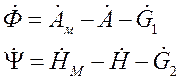 когда время адаптации подстройки рег-ра << чем период на протяжении которого могут изменится элементы матриц А и Н

  

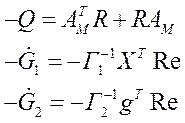
В соответствии с этими 3-мя уравнениями мы находим предыдущее.