Ответы на экзаменационные билеты № 1-30 дисциплины "Адаптивные системы управления" (Математическое описание сигналов и операторов в непрерывных линейных детерминированных системах. Адаптивные системы управления), страница 12

1. Для линейного непрерывного стационарного объекта на основе классического интегрального критерия.

Рассмотрим простейший вариант. Пусть объект описывается линейной, стационарной, детерминированной моделью, без запаздывания.

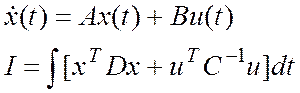
Пусть существует функция , которая соответствует экстремальным значениям в каждый момент времени. Когда существует такая функция и есть ее значения, тогда эти значения можно аппроксимировать некоторой математической функцией. D, C – матрицы весовых коэффициентов, которые определяют роль отдельных переменных в составе подынтегральной функции. Зададимся . Тогда имеем: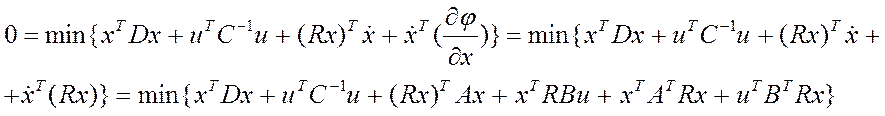

Берем частную производную по u и приравниваем ее к 0. Получаем оптимальное управление: . Для нахождения матрицы R подставляем u_опт в исходный критерий. Тогда имеем:

2. Для линейного непрерывного стационарного объекта на основе критерия обобщенной работы.

Критерий обобщенной работы:   J=∫ [X^TDX+X^TRBCB^TRX+U^TC^-1U]dt

Рассмотрим синтез системы с таким критерием:

=Ax+Bu

J=∫ [X^TDX+X^TRBCB^TRX+U^TC^-1U]dt

Будем искать оптимальный закон управления и неизвестную матрицу R.

Найдем    Min=φ=X^TRX.

Дальше используем ур-ние Белмана :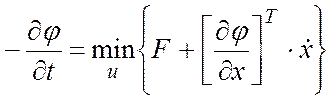  

A,B,C,D –не зависят от времени ; R – также, тогда имеем :

0 = min { X^TDX+X^TRBCB^TRX+U^TC^-1U+(RX)^T(AX+BU)+(AX+BU)^TRX }

0 = min { X^TDX+X^TRBCB^TRX+U^TC^-1U+X^TRAX+X^TRBU+X^TA^TRX+U^TB^TRX }

Дальше берем производную : 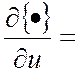 C^-1U+C^-1U+B^TRX+B^TRX

Находим U_опт = -СB^TRX

Подставим закон управления в функц-ое ур-ние :

0 =  X^TDX+X^TRBCB^TRX+X^TRBCB^TRX+X^TRAX–X^TRBCB^TRX+X^TA^TRX–X^TRBCB^TRX 0 =  X^TDX+X^TRAX+X^TA^TRX

Можно сказать, что все составляющие имеют общие множители X^T и X, поэтому 0 можно домножить на X^T и X и сократить : 0 =  D+RA+A^TR.

Отсюда находим матрицу R.

ТАУ 27-2

Если бы объединить последние 2 составляющие , тогда   0 = D+

И тогда  

Такой подход был предложен Красовским А.А.

3. Для линейного непрерывного стационарного объекта подверженного измеряемым возмущениям.

Рассмотрим синтез такой системы :  = Ax+Bu

J=∫ [X^TDX + U^TC^-1U]dt

X = X_факт – X_жел   ,  F – воздействие  .

Используем ур-ние Белмана для непрерывной системы: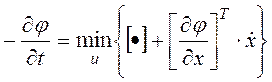

[·] – подинтегральная ф-ция .

Зададимся ф-цией    φ = X^TRX + LX + X^TL  , где R=R^T , L=L^T

Т.к. матрицы не зависят от времени, тогда :

0 = min { X^TDX+U^TC^-1U+(RX+L)^T(AX+BU)+(AX+BU)^T( RX+L) }

0=min{X^TDX+U^TC¹U+X^TRAX+X^TRBU+X^TRF+LAX+LBU+LF+X^TA^TRX+ +X^TA^TL+ U^TB^TRX + U^TB^TL+F^TRX+ F^TL }

Дальше берем производную от {·} и = 0 :     0=C¹U+C¹U+B^TRX+B^TL+B^TRX+B^TL

U_опт = - CB^TRX – CB^TL  ;   U^T_опт = - X^TRBC – LBC

Подставим в функц-ое ур-ние закон управления :  

При том, что   U^TC^-1U = -[ X^TRBC + LBC ]C^-1[ CB^TRX + CB^TL ]

U^TC^-1U = X^TRBCB^TRX+X^TRBCB^TL+LBCB^TRX+LBCB^TL

0 =  X^TDX+ X^TRBCB^TRX+X^TRBCB^TL+ LBCB^TRX+LBCB^TL+ X^TRAX–          X^TRBCB^TRX– X^TRBCB^TL+X^TRF+LAX– LBCB^TRX–LBCB^TL+LF+ X^TA^TRX+ +X^TA^TL – X^TRBCB^TRX–  LBCB^TRX– X^TRBCB^TL– LBCB^TL+F^TRX+F^TL       

Собираем составляющие с одинаковыми множителями :

X^T·0·X = X^TDX+ X^TRAX+ X^TA^TRX– X^TRBCB^TRX          

X^T·0 = X^TRF+X^TA^TL– X^TRBCB^TL

0·X = LAX+ F^TRX–LBCB^TRX

0 = LF+ F^TL– LBCB^TL

Сокращаем иксы :

1)  0 = D+ RA+ A^TR–RBCB^TR  → R

2)  0 = RF+A^TL– RBCB^TL

3) 0 = LA+ F^TR–LBCB^TR

4) 0 = LF+ F^TL– LBCB^TL  →  L

Отсюда  L = F^TR· [BCB^TR–A]^-1

Подставим в закон управления :

U_опт = - CB^TRX – CB^TF^TR· [BCB^TR–A]^-1

 

 

 

 

 

 

 

ТАУ 27-3

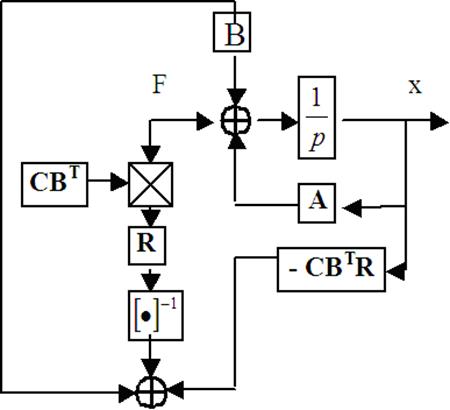
4. Для линейного непрерывного стационарного объекта с запаздыванием по каналу управления.

(t) = A·x(t) + B·u(t-τ)

Построим структуру объекта. Задача: попробовать математическими переходами спрятать элемент с запаздыванием за другими переменными.

 

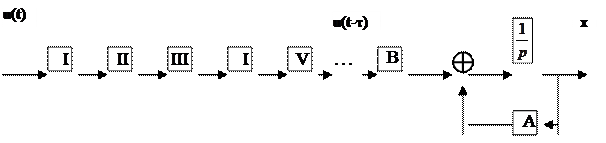Пусть каждый из введенных блоков имеет элементарное звено 1-го порядка.

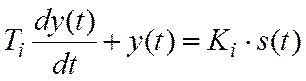
Видим, что чем больше апериодич. звеньев, то больше получается запаздывание. Т.о. можно получить u(t) на входе в систему той же амплитуды, изменяются T_i и K_i.

W_зап.(p) = e^-pτ

Можно разбить запаздывание на экспоненты:   e^-p·0.2τ · e^-p·0.2τ · ….

Экспоненту можно разложить в ряд:    e^-p·0.2τ = =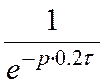

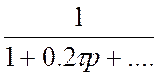
Ограничимся двумя составляющими.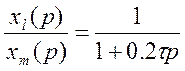 

Дальше можно перейти на ДУ 1-го порядка: