Ответы на экзаменационные билеты № 1-30 дисциплины "Адаптивные системы управления" (Математическое описание сигналов и операторов в непрерывных линейных детерминированных системах. Адаптивные системы управления), страница 9

  

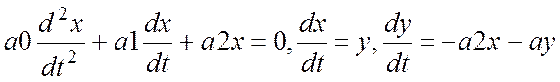
Если есть н.у. можно построить временную характеристику.

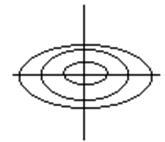
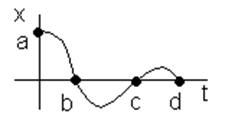Глядя на такую характеристику можно сказать, что корни будут комплексные с вещественной частью меньше 0. Если х будет уменьшаться, то у относительной точки М0 будет или возрастать, или убывать(будет колебаться). Так будет до тех пор пока х не станет =0. Все траектории будут иметь спиралевидную форму и фокусироваться в начале координат. Эти графики получили название типа фокус.

                                                        

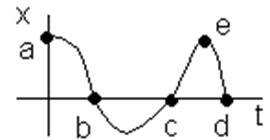
- фазовый портрет типа центр.

Возьмем другой переходной процесс который монотонно затухает :

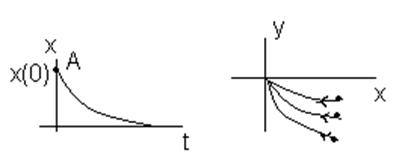- фазовый портрет типа узла все характеристики сходятся в одной т. Если стрелки к узлу значит устойчивая.

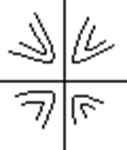
Пусть у системы 1 корень а второй т.е. система не устойчива, но один корень будет стремиться попасть в узел а другой наоборот выйти из узла.

- фазовый портрет типа седло.

ТАУ 20. Метод гармонической линеаризации и его использование при

анализе и синтезе систем управления.

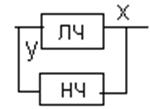
y=f(x)- нелинейное звено, зависит от аргумента независим от времени. На вход НЭ сигнал х может быть произвольной формы этот сигнал можно разложить на элементарные ф-ции x=asinwt-выходной сигнал нелинейного звена у можно разложить в ряд Фурье 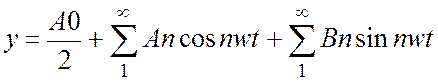, далее сигнал у уприрается в линейную часть. Линейная часть обрежет высокие составляющие, отфильтрует гармоники выше 1-й, тогда 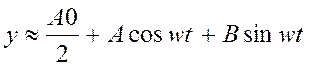,,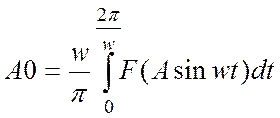 если колебания будут симметричны, то А0=0,

, .

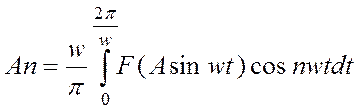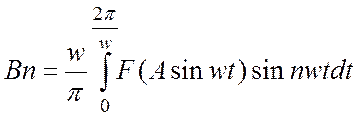Для 1-й гармоники , в симметричных колебаниях А= 

         заменим ,:,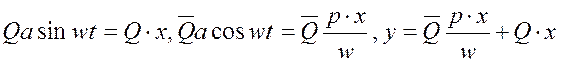

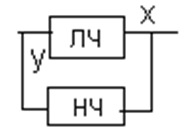Отсюда мы пришли в область линейных систем, выполнив линеаризацию на основе гармонического баланса.

Для нелинейных систем такого вида можно найти параметры н.э.

Вначале была зависимость y=F(x), затем находим W(p) за счет появления временного аргумента. Wн.э=q+jq’-необходимо найти коэффициенты q и q’

       

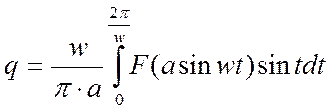
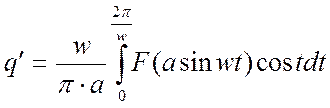
Произведем замену:           ,    .

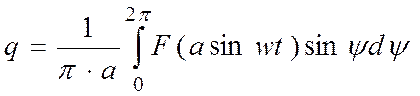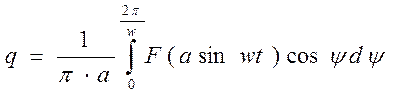В зависимости от того, какого типа нелинейность и нелинейность относительно нач координат, то

,   

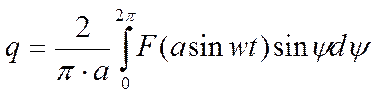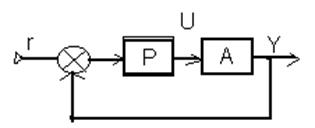ТАУ 21-1. Синтез дискретных компенсационных регуляторов из условия обеспечения желаемого времени регулирования.                 Для объектов без запазд-я

W=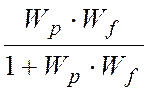 Пусть структура регулятора будет свободной. Пусть необходимо чтобы на выходе системе получили желаемый результат за m тактов: Y(mT)=r(0), r(0)=1(kT)   r(Z)=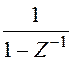

Будем считать, что нам объект инертный на начальном такте на выходе отсутствует сигнал, тогда:

Y(Z)= 

Аналогично для выхода регулятора:

Необходимо сократить насколько слагаемых

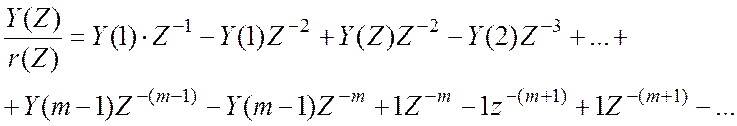
Начиная с элемента 1Z остальные элементы уничтожаются т.к. они подобны получаем полином

P(Z)=Y(1)Z-1Z

Q(Z)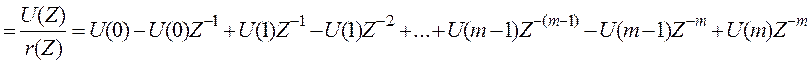

Принимаем полиномы:

Р(Z)=P1Z             Q(Z)=Q0+Q1Z

P1=Y(1)                                                            Q0=U(0)

P2=Y(2)-Y(1)                                                   Q1=U(1)-U(0)

.                                                                                   ….

Pm=Y(m)-Y(m-1)=1-Y(m-1)                           Qm=U(m)-U(m-1)

                                                      

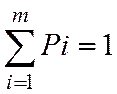
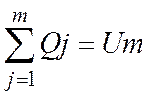
Мы можем найти передаточную ф-цию нашего объекта:

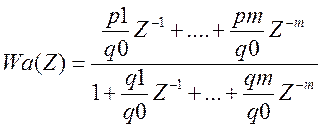
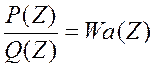 c другой стороны нам дана передаточная ф-ция объекта:

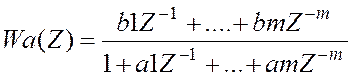
Разделим все коэффициенты на Q0 и получим                  à

ТАУ 21-2

          

   

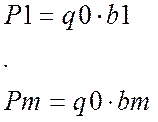
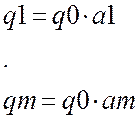
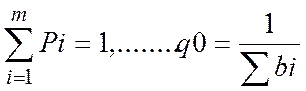
Вернемся к нашей передаточной ф-ции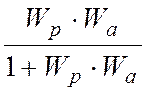 Wзс=     WзсP(Z)

P(Z)= 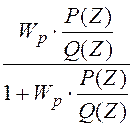 неизвестная Wp

P(Z)+P(Z)W(p)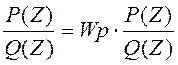 

P(Z)=Wp*()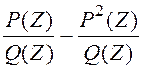

1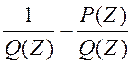=Wp*()         Wp=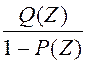получили передаточную ф-цию регулятора

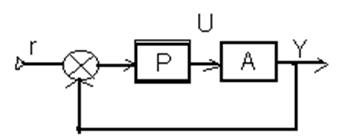Для объектов с запаздыванием

W=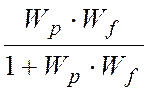 Пусть структура регулятора будет свободной. Пусть необходимо чтобы на выходе системе получили желаемый результат за m тактов: Y(mT)=r(0),r(0)=1(kT)   r(Z)=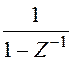

Будем считать, что нам объект инертный на начальном такте на выходе отсутствует сигнал, тогда:

Y(Z)= 

Аналогично для выхода регулятора:

Необходимо сократить насколько слагаемых

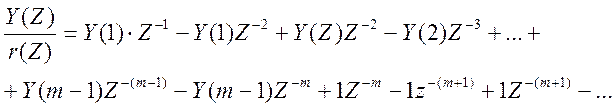
Начиная с элемента 1Z остальные элементы уничтожаются т.к. они подобны получаем полином

ТАУ 21-3

P(Z)=Y(1)Z--1Z

Q(Z)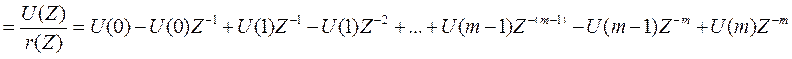

Принимаем полиномы:

Р(Z)=P1Z      Q(Z)=Q0+Q1Z

P1=Y(1)                                        Q0=U(0)

P2=Y(2)-Y(1)                               Q1=U(1)-U(0)

.                                            ….