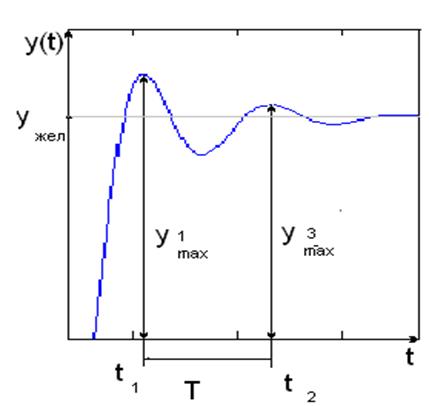
Быстродействие- время, в течение которого переходная характеристика войдёт в доверительный интервал и уже не выйдет, это время и есть время регулирования tрег.
Перерегулирование – максимальная амплитуда А1. Если перейти к безразмерным единицам, то перерегулирование будет характеризоваться следующим фактором:
.
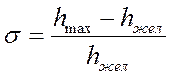Степень затухания- данный показатель получаем сопоставляя амплитуды переходной характеристики следующим образом:
.
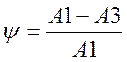Можно также посчитать кол-во колебаний в системе n. Хорошая система та система, в которой переходной процесс затухает за 4 колебания.
Косвенные критерии качества регулирования.
1) Переходной процесс существенно зависит от корней характеристического уравнения. Для оценки качества регулирования используется понятие “средний геометрический корень”- Ω.
,
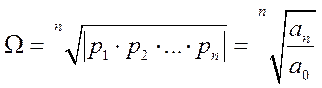где
p1..pn – корни характеристического уравнения, а 
- соответствующие коэффициенты д.у.
Чем больше величина Ω , тем у системы большее быстродействие. Если допустить что корни вещественные и отрицательны, то корень, кот. в координатах Im(Re) будет ближе к нимой оси, будет затягивать переходной процесс.
Если ближайший корень к мнимой оси будет следующим:
, тогда
переходной процесс будет затягиваться этой парой корней и решение будет
зависеть от p1,2.
Перейдём к след. Виду
ТАУ 12-2
;
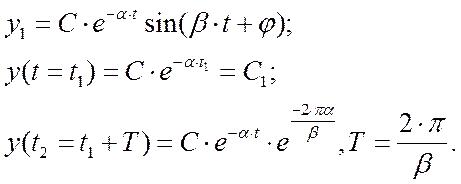
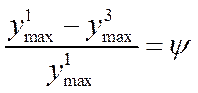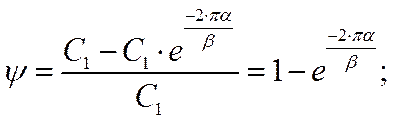
ψ – степень затухания.
Зная значение комплексного корня можно определить степень затухания.
|
Построим для замкнутой системы АФЧХ. Если полученная характеристика не охватывает точку с координатами (-1,0), то система является устойчивой. Оценим запас устойчивости системы. Расстояние от точки пересечения АФЧХ с отрицательной вещественной осью до точки (-1,0) будет амплитудой запаса устойчивости – γ, а угол, который составит луч, выходящий из начала координат и пересекающий точку АФЧХ, лежащую ближе всего к точке (-1,0) (по вещественной координате), с отрицательной вещественной осью – запас устойчивости по фазе – φ.
Можно построить частотные хар-ки и другого плана.
Если
мы имеем передаточную хар-ку системы, то можно выделить действительную и мнимую
части.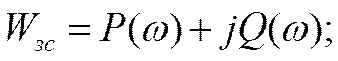 
Если построить хар-ку P(ω) и она будет монотонна, то значит в системе будет невысокое перерегулирование, а время переходного процесса будет определяться частотой среза.
Можно
оценить модуль Wзс -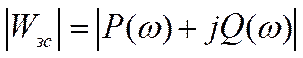 
.
Построив зависимость модуля з.с. от частоты, мы найдём максимум - показатель колебательности – М.
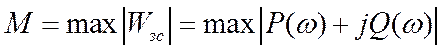
При М=1,1..1,3 – система имеет хорошее качество.
Пусть
ТАУ 12-3
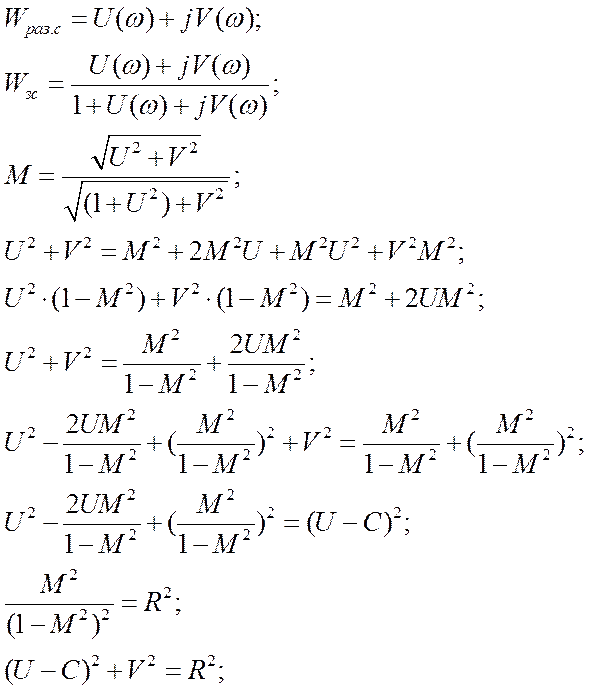
В результате получили уравнение окружности с радиусом R и с центром в точке (C,0):
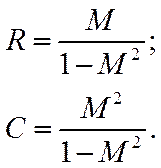
В книгах существуют монограммы, на которых изображены окружности соответствующие определённому показателю колебательности. Если Wраз.с будет касаться окружности соответствующей некоторому показателю колебательности, то этот показатель и будет критерием данной системы.
ТАУ 13-1. Синтез системы управления метод расчета параметров регулятора на желаемую степень затухания переходного процесса.
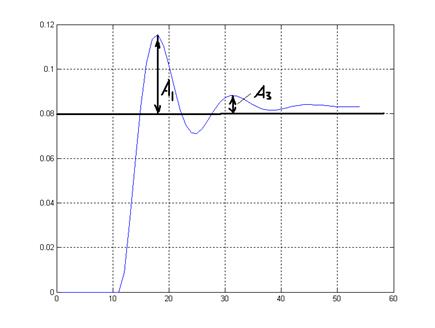Имеем переходную характеристику:
Степень
затухания ПП: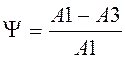 
.
Пусть есть одно условие – yжел.. Другое – пусть структура регулятора (т.е. закон регулирования) известна.
Пусть есть корни:
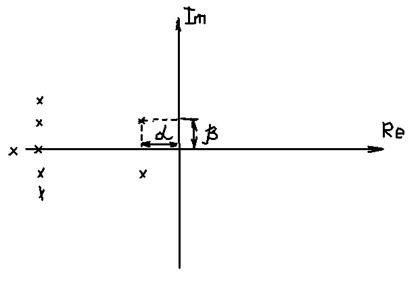
y = 1- е-2pb/a
b/a - колебательность
b/a=m
y = 1- е-2pm
Колебательность b/a=m, m=0,221…0,3 при yжел=0,75…0,9.
Предположим, что наша система невысокого порядка.
Синтезируем П-регулятор:
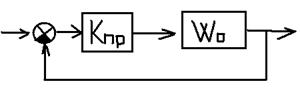
Пусть ось, где находятся корни, совпадает с мнимой
осью, т.е. Re=0, т.е. система находится на границе устойчивости. По
критерию Найквиста:
. (АФЧХ пойдет через(-1;j0)).
Сместим Im к желаемому корню, тогда: 
(1)
[если регулятор более общий: 
(2)]
Нужно найти коэффициент пропорциональности, чтобы он удовлетворял (1)
КПРRe(j,w)=-1; КПР,w – ? Можно записать в показательной форме:
;
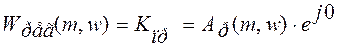
В (2):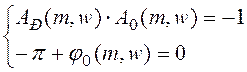 
Þ
. Т.е. можно найти КПР.ЖЕЛ.
Передаточная
ПИ-регулятора имеет вид: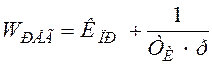
. В зависимости от частоты и m:
. Получим
систему уравнений:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.