Данный раздел содержит краткие сведения из теории линейных систем, которые понадобятся при изучении курсов «Статистическая радиотехника» и «Основы теории случайных процессов». Для повторения материала, изложенного в данном подразделе, следует обратиться к учебникам С.И. Баскакова [6] или И.С. Гоноровского [7].
 Пусть некоторая система преобразует
известную функцию времени
Пусть некоторая система преобразует
известную функцию времени ![]() (входной
процесс) в выходную функцию времени
(входной
процесс) в выходную функцию времени ![]() (выходной
процесс), где
(выходной
процесс), где ![]() – оператор, определяемый
свойствами системы. Схема работы такой системы условно показана на рис. 1.1.
В общем случае система может быть многоканальной, имеющей несколько входов и
выходов. В этом случае входной и выходной процессы можно рассматривать как
векторные процессы. Далее будем оператором называть правило
– оператор, определяемый
свойствами системы. Схема работы такой системы условно показана на рис. 1.1.
В общем случае система может быть многоканальной, имеющей несколько входов и
выходов. В этом случае входной и выходной процессы можно рассматривать как
векторные процессы. Далее будем оператором называть правило ![]() , согласно которому входной процесс
, согласно которому входной процесс ![]() преобразуется в выходной процесс
преобразуется в выходной процесс ![]() , где процессы
, где процессы ![]() и
и ![]() в общем случае могут быть векторными.
в общем случае могут быть векторными.
Система называется линейной,
если для нее справедлив принцип суперпозиции, т.е. когда реакция
линейной системы на входной процесс 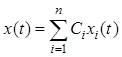 определяется соотношением
определяется соотношением
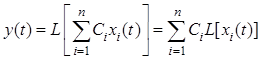 при любых весовых коэффициентах
при любых весовых коэффициентах ![]() ,
, ![]() , при
любых входных процессах
, при
любых входных процессах ![]() ,
, ![]() (которые могут быть детерминированными или
случайными процессами), а также при любых значениях
(которые могут быть детерминированными или
случайными процессами), а также при любых значениях ![]() . Формула
показывает, что выходной процесс
. Формула
показывает, что выходной процесс ![]() линейной системы, представляющий собой
результат линейного преобразования взвешенной суммы входных процессов
линейной системы, представляющий собой
результат линейного преобразования взвешенной суммы входных процессов ![]() ,
, ![]() , равен
взвешенной сумме результатов преобразования каждого из входных процессов тем же
линейным оператором.
, равен
взвешенной сумме результатов преобразования каждого из входных процессов тем же
линейным оператором.
Отметим, что из формулы следует, что при нулевом воздействии реакция линейной системы равна нулю, т.е.
![]() .
.
Например, линейными операторами являются операторы дифференцирования:
![]() , интегрирования:
, интегрирования:
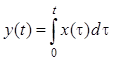 , умножения на некоторую вполне
определенную неслучайную функцию
, умножения на некоторую вполне
определенную неслучайную функцию ![]() :
:
![]() , интегрирования с определенной весовой
функцией
, интегрирования с определенной весовой
функцией ![]() :
:
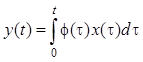
и так далее. К линейным системам, например, могут быть отнесены такие радиотехнические устройства, как усилители, фильтры, линии задержки и т.п.
В общем случае система или оператор, определяющий ее свойства, называются нелинейными, если для них не применим принцип суперпозиции. К числу нелинейных относятся такие радиотехнические системы и устройства, как автогенераторы, детекторы, перемножители и др. Практически все радиотехнические системы становятся нелинейными при чрезмерно больших значениях входных сигналов. Например, в линейных усилителях рано или поздно наступает ограничение выходного сигнала при увеличении амплитуды входного. Однако их можно считать линейными для некоторой ограниченной области амплитуд входных сигналов.
В ряде радиотехнических
задач приходится иметь дело с операторами ![]() ,
которые представляют собой сумму линейного преобразования входного процесса
,
которые представляют собой сумму линейного преобразования входного процесса ![]() и некоторой заданной функции
и некоторой заданной функции ![]() :
:
![]() , или в частном случае константы с:
, или в частном случае константы с:
![]() .
.
Очевидно, что для операторов и не выполняется принцип суперпозиции.
Однако в ряде случаев при анализе систем, описываемых ![]() ,
достаточно решить эту задачу только для линейного оператора
,
достаточно решить эту задачу только для линейного оператора ![]() . Например, известно, что ковариационная
функция случайного процесса не меняется при прибавлении к нему
детерминированной функции
. Например, известно, что ковариационная
функция случайного процесса не меняется при прибавлении к нему
детерминированной функции ![]() , а его математическое
ожидание изменится на
, а его математическое
ожидание изменится на ![]() [5]. Поэтому операторы и выделены в отдельный класс и называются
линейными неоднородными операторами.
[5]. Поэтому операторы и выделены в отдельный класс и называются
линейными неоднородными операторами.
Линейная система называется стационарной (система с постоянными параметрами), если сдвиг входного сигнала приводит к тому же сдвигу выходного сигнала
![]() .
.
Предположение о постоянстве параметров выполняется для многих радиотехнических систем.
Функция ![]() называется собственной для линейной
системы, если она проходит через линейную систему без изменения формы, меняя
лишь масштаб и претерпевая задержку. Реакция линейной системы на собственную
функцию определяется собственным значением, определяющим изменение масштаба и
величину задержки собственной функции на частоте
называется собственной для линейной
системы, если она проходит через линейную систему без изменения формы, меняя
лишь масштаб и претерпевая задержку. Реакция линейной системы на собственную
функцию определяется собственным значением, определяющим изменение масштаба и
величину задержки собственной функции на частоте ![]() .
.
Для стационарной линейной системы собственными функциями являются комплексные функции вида
![]() , где
, где ![]() –
мнимая единица. Собственными значениями стационарной линейной системы являются
комплексные величины
–
мнимая единица. Собственными значениями стационарной линейной системы являются
комплексные величины
![]() , определяющие отклик линейной системы
на экспоненциальный комплексный сигнал на частоте
, определяющие отклик линейной системы
на экспоненциальный комплексный сигнал на частоте ![]() .
Функция частоты
.
Функция частоты ![]() называется комплексной
частотной характеристикой линейной стационарной системы, а
называется комплексной
частотной характеристикой линейной стационарной системы, а ![]() и
и ![]() – амплитудно-частотная
и фазочастотная характеристики этой системы. Здесь и далее точка сверху
обозначает, что
– амплитудно-частотная
и фазочастотная характеристики этой системы. Здесь и далее точка сверху
обозначает, что ![]() является комплексной функцией.
Амплитудно-частотная характеристика определяет изменение амплитуды (масштаба)
собственной функции, а фазочастотная характеристика – задержку. Отметим, что
комплексная частотная характеристика линейной системы с постоянными параметрами
не зависит ни от времени, ни от вида входного сигнала.
является комплексной функцией.
Амплитудно-частотная характеристика определяет изменение амплитуды (масштаба)
собственной функции, а фазочастотная характеристика – задержку. Отметим, что
комплексная частотная характеристика линейной системы с постоянными параметрами
не зависит ни от времени, ни от вида входного сигнала.
Отклик системы ![]() выражается преобразованием Фурье от
выражается преобразованием Фурье от
![]() , где
, где ![]() и
и ![]() –
спектральные плотности входного и выходного процессов,
–
спектральные плотности входного и выходного процессов, ![]() –
прямое преобразование Фурье.
–
прямое преобразование Фурье.
Особую роль в теории линейных систем играет воздействие в форме дельта-функции [5]
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.