Применение теории случайных процессов, страница 16

может быть представлена как сумма двух синусоид, сдвинутых одна относительно другой на . Такую импульсную характеристику можно реализовать с помощью линейной системы, структурная схема которой приведена на рис. 3.3. Эта схема отличается от аналогичной схемы согласованного фильтра для видеоимпульса тем, что идеальный интегратор заменен высокодобротным резонансным  контуром с резонансной частотой , а вычитающее устройство заменено сумматором.

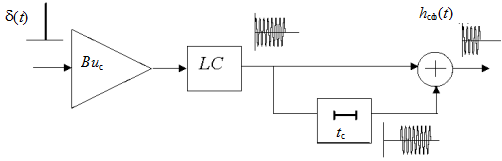
Рис. 3.3

Энергия полезного сигнала :

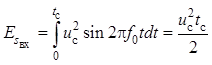, тогда отношение сигнал/шум для фильтра, согласованного с прямоугольным радиоимпульсом, определяется следующим соотношением:

.                                   

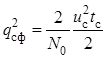Подставив в , получим корреляционную функцию входного сигнала

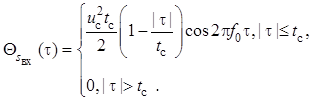
Как и следовало ожидать, форма огибающей корреляционной функции прямоугольного радиоимпульса совпадает с корреляционной функцией прямоугольного видеоимпульса. Из следует, что сигнал и ковариационная функция шума на выходе фильтра, согласованного с прямоугольным радиоимпульсом, соответственно равны:

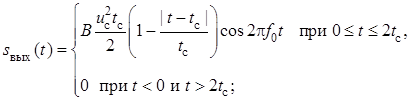
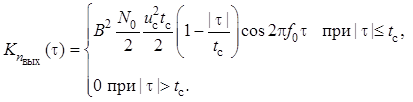
Для оценки интервала корреляции используем огибающую ковариационной функции  [5], тогда, так же как и для видеоимпульса,

.

3.1.5.4. Квазиоптимальный фильтр для прямоугольного радиоимпульса

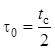В качестве квазиоптимального фильтра для прямоугольного радиоимпульса возьмем высокодобротный колебательный контур с импульсной характеристикой . Комплексная частотная характеристика такого контура

, где 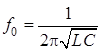 – резонансная частота.

Максимум амплитуды полезного сигнала на выходе высокодобротного колебательного контура при действии на его входе прямоугольного радиоимпульса достигается в момент окончания радиоимпульса:

.                        

Дисперсия шума на выходе высокодобротного колебательного контура при действии на его входе белого шума в соответствии с будет

.                          

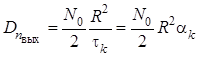Разделив квадрат максимального значения сигнала на дисперсию шума , получим

.                          

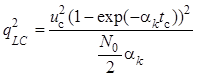С учетом приведем выражение к виду

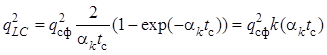, где  – отношение сигнал/шум для оптимального фильтра, согласованного с прямоугольным радиоимпульсом. Очевидно, что график зависимости  совпадает с графиком, приведенным на рис. 3.2. Таким образом, так же как и для интегрирующей RC-цепи, оптимальное значение постоянной времени высокодобротного параллельного контура

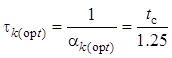, при этом проигрыш в отношении сигнал/шум оптимальному фильтру

.

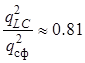Из приведенных в данном разделе примеров следует, что квазиоптимальные фильтры для прямоугольных видеоимпульсов и радиоимпульсов незначительно проигрывают оптимальным фильтрам в отношении сигнал/шум, при этом их реализация оказывается существенно проще. Однако найти такие простые и в то же время эффективные квазиоптимальные фильтры удается в достаточно редких случаях. Например, если мы будем использовать интегрирующую RC-цепь в качестве квазиоптимального фильтра для последовательности из  видеоимпульсов, проигрыш квазиоптимального фильтра оптимальному будет расти с увеличением .

3.1.6. Плотность распределения вероятностей сигнала на выходе согласованного фильтра

Найдем плотность распределения вероятностей  сечения случайного процесса

на выходе согласованного фильтра в момент времени . Согласованные фильтры являются фильтрами нижних частот, в которых происходит нормализация белого шума, т.е. плотность распределения вероятностей случайного процесса на выходе согласованного фильтра является гауссовской. Поэтому достаточно найти математическое ожидание и дисперсию сечения случайного процесса . Используя теоремы, приведенные в [5], получим

,

.

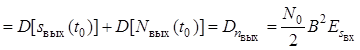Отсюда следует, что

.

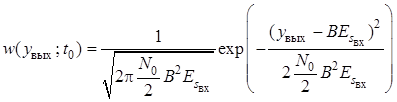Если на входе согласованного фильтра действует только шум, а информационный сигнал отсутствует, то , а дисперсия останется неизменной. В этом случае

.

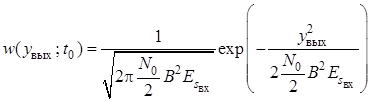Таким образом, отсутствие информационного сигнала на входе согласованного фильтра приводит к смещению плотности распределения вероятностей сечения выходного случайного процесса, взятого в момент времени , влево на величину, равную энергии сигнала, умноженную на константу . При этом дисперсия остается неизменной. Это свойство широко используется в теории обнаружения сигналов.