Применение теории случайных процессов, страница 5

Следовательно, спектральная плотность мощности процесса на выходе линейной системы в установившемся режиме равна произведению спектральной плотности мощности входного процесса и квадрата амплитудно-частотной характеристики линейной системы. Подчеркнем, что спектральная плотность мощности выходного процесса не зависит от фазочастотной характеристики линейной системы.

Дисперсия выходного случайного процесса с учетом определяется соотношением [5]

.                  

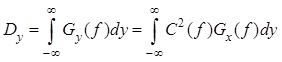Из формул , и следует, что дисперсия выходного процесса  зависит от ковариационной функции входного процесса , поскольку мощность выходного процесса зависит как от амплитудно-частотной характеристики  линейной системы, так и от спектральной плотности мощности  входного процесса.

2.3. Взаимные ковариационная функция

и спектральная плотность мощности

процессов на входе и выходе

линейной системы

Вначале найдем взаимную ковариационную функцию случайных процессов на входе и выходе линейной каузальной системы при условии, что входной случайный процесс  начинает воздействовать на эту систему в момент времени , т.е. для переходного режима. Затем найдем аналогичные соотношения для установившегося режима и некаузальной линейной системы.

Перемножив центрированные [5] входной  и выходной  процессы линейной системы, взяв математическое ожидание и затем поменяв местами операции взятия математического ожидания и интегрирования, получим для переходного режима следующее выражение:

.

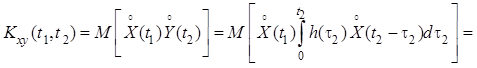
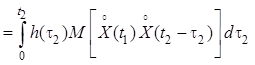Отсюда следует, что взаимная ковариационная функция входного процесса , который начинает действовать на стационарную линейную каузальную систему в момент времени , и отклика  равна:

.                  

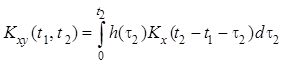Из получим формулу для взаимной ковариационной функции стационарных процессов на входе и выходе линейной каузальной системы в установившемся режиме, т.е. при :

.          

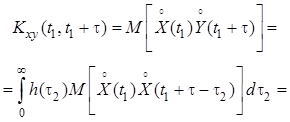
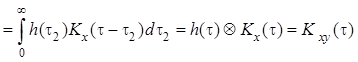Аналогичным образом получим формулу для взаимной ковариационной функции стационарных процессов на входе и выходе некаузальной линейной системы в установившемся режиме:

.                            

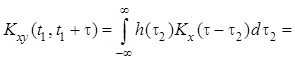
Из формул и следует, что в установившемся режиме стационарные процессы  и  являются стационарно связанными в широком смысле случайными процессами [5] и их взаимная ковариационная функция равна интегралу свертки ковариационной функции входного процесса и импульсной характеристики линейной системы.

Взяв преобразование Фурье от левой и правой частей или и выполнив преобразования, аналогичные тем, что были выполнены при выводе формулы , получим

.                              

Из следует, что взаимная спектральная плотность мощности зависит от комплексной частотной характеристики линейной системы (т.е. зависит как от амплитудно-частотной, так и от фазочастотной характеристики) и в общем случае является комплексной функцией частоты.

2.4. Воздействие белого шума

на линейную систему

Пусть входным процессом линейной системы является белый шум [5] с ковариационной функцией и спектральной плотностью мощности вида:

,                                  

.                                     

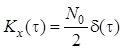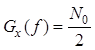Математическое ожидание белого шума равно нулю.

Подставив в формулы и и используя фильтрующее свойство дельта-функции, получим ковариационную функцию и дисперсию процесса на выходе линейной системы в переходном режиме:

       

.                              

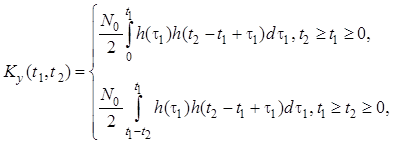
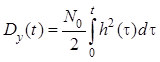В учтено свойство импульсной характеристики каузальной линейной системы.

В установившемся режиме формулы и имеют следующий вид:

                  

.                                

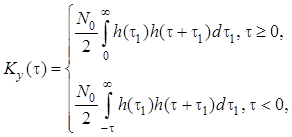
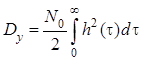Для некаузальной линейной системы в установившемся режиме ковариационная функция и дисперсия выходного процесса с учетом формул и имеют вид

,                      

.                               

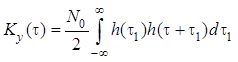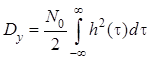Применительно к белому шуму спектральная плотность мощности выходного процесса с учетом определяется формулой

.                                

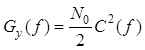Таким образом, при воздействии на стационарную линейную систему белого шума спектральная плотность мощности процесса на ее выходе с точностью до константы  равна квадрату амплитудно-частотной характеристики этой системы.