Применение теории случайных процессов, страница 19

Тогда соответствующие спектральные плотности мощности имеют вид [5]

,                            

.                                  

Подставляя и в и , получим комплексную частотную характеристику фильтра Винера и величину минимальной среднеквадратической ошибки:

,                     

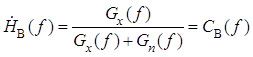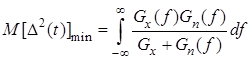,                      где  – амплитудно-частотная характеристика фильтра Винера.

Из полученных соотношений следует:

1.  Так как спектральные плотности мощности являются вещественными и четными функциями, то комплексная частотная характеристика фильтра Винера также является вещественной и четной. Откуда следует, что фазочастотная характеристика фильтра Винера тождественно равна нулю на всех частотах. Таким образом, фильтр Винера не вносит фазовых искажений в наблюдаемый сигнал и тем самым максимально сохраняет форму оцениваемого сигнала.

2.  Амплитудно-частотная характеристика фильтра Винера

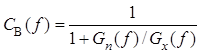
примерно равна единице на тех частотах, где спектральная плотность мощности оцениваемого сигнала много больше спектральной плотности мощности шума () и примерно равна нулю при .

3.  Поскольку преобразование Фурье от четной функции является четной функцией, импульсная характеристика фильтра Винера является также четной функцией.

4.  Минимальная cреднеквадратическая ошибка определяет потенциальную границу точности линейной фильтрации случайного процесса, наблюдаемого на фоне аддитивного шума, не коррелированного с этим процессом. При этом величина cреднеквадратической ошибки не превышает дисперсии шума:

.

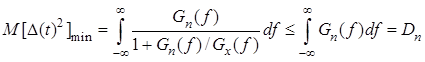Очевидно, что среднеквадратическая ошибка равна дисперсии шума, если фильтр вообще отсутствует, т.е. когда . Поэтому использование фильтра Винера не может привести к увеличению среднеквадратической ошибки.

5.  Из следует, что среднеквадратическая ошибка фильтрации равна нулю при , т.е. при отсутствии шума или когда спектральные плотности мощности сигнала и помехи не перекрываются на всех частотах. В последнем случае амплитудно-частотная характеристика фильтра Винера равна

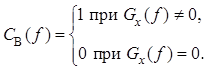
6.  Если спектральные плотности мощности сообщения и помехи перекрываются, например, при , то среднеквадратическая ошибка фильтрации не равна нулю. Ошибка фильтрации возникает как от пропускания помехи в частотном диапазоне , так и от ослабления сигнала в этом же частотном диапазоне. Причем чем больше спектральная плотность мощности помехи в диапазоне перекрытия, тем сильнее искажение информационного сигнала.

7.  Если спектральная плотность мощности помехи с точностью до константы равна спектральной плотности мощности информационного сигнала, т.е. , то фильтр Винера вырождается в линейный усилитель с постоянным во всем диапазоне частот коэффициентом усиления

.

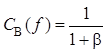Пример 3.1. Пусть сигнал с ковариационной функцией

                              наблюдается на фоне аддитивного белого шума с ковариационной функцией

.                                  

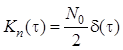Математические ожидания сигнала и шума равны нулю. Сигнал и шум взаимно некоррелированные случайные процессы [5]. Выполнить синтез и анализ фильтра Винера.

Спектральные плотности мощности сигнала и помехи соответственно равны:

,                              

.                                     

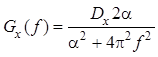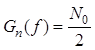Введем безразмерный коэффициент , имеющий физический смысл отношения сигнал/шум в эффективной полосе частот. Эффективная ширина спектра сообщения  равна [5]

, тогда дисперсия шума в эффективной полосе частот

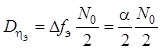, откуда

.

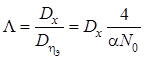Подставив и в и , получим

,          

.          

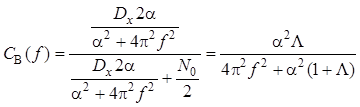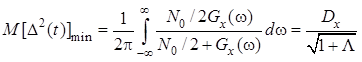Из и следует, что при неограниченном увеличении отношения сигнал/шум в эффективной полосе частот () амплитудно-частотная характеристика фильтра Винера стремится к единице на всех частотах, т.е. фильтр будет пропускать сигнал без искажений, при этом среднеквадратическая ошибка стремится к нулю. С другой стороны, при неограниченном уменьшении отношения сигнал/шум в эффективной полосе частот амплитудно-частотная характеристика фильтра Винера на всех частотах стремится к нулю. В этом случае оптимальное значение сигнала на выходе фильтра равно нулю. Расширение эффективной ширины спектра сообщения, наблюдаемого на фоне аддитивного белого шума, при фиксированном значении его мощности () приводит к уменьшению  и, как следствие, к увеличению среднеквадратической ошибки. Это объясняется тем, что спектрально-корреляционные характеристики сообщения приближаются к спектрально-корреляционным характеристикам шума и их невозможно разделить с помощью линейной фильтрации. ■