Приравняв ![]() к нулю
в , найдем дисперсию шума на выходе
согласованного фильтра
к нулю
в , найдем дисперсию шума на выходе
согласованного фильтра
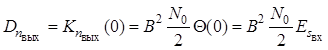 , которая, так же как и амплитуда
сигнала на выходе согласованного фильтра,
пропорциональна энергии входного сигнала. Отношение сигнал/шум на выходе
согласованного фильтра в момент времени
, которая, так же как и амплитуда
сигнала на выходе согласованного фильтра,
пропорциональна энергии входного сигнала. Отношение сигнал/шум на выходе
согласованного фильтра в момент времени ![]() равно
равно
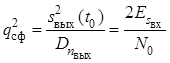 .
.
При белом шуме отношение сигнал/шум на
выходе согласованного фильтра определяется двумя физическими величинами –
энергией полезного сигнала ![]() и интенсивностью белого
шума
и интенсивностью белого
шума ![]() , т.е. зависит от характеристик входного
сигнала и входного шума. Таким образом, потенциально достижимое
отношение сигнал/шум можно найти, не выполняя синтез согласованного фильтра.
Кроме того, есть два очевидных способа улучшения отношения сигнал/шум. Первый состоит
в увеличении энергии передаваемого сигнала, а второй – в снижении интенсивности
шума.
, т.е. зависит от характеристик входного
сигнала и входного шума. Таким образом, потенциально достижимое
отношение сигнал/шум можно найти, не выполняя синтез согласованного фильтра.
Кроме того, есть два очевидных способа улучшения отношения сигнал/шум. Первый состоит
в увеличении энергии передаваемого сигнала, а второй – в снижении интенсивности
шума.
Если на вход фильтра, согласованного с![]()
![]() , подать любой другой
детерминированный сигнал
, подать любой другой
детерминированный сигнал ![]() , то выходной сигнал будет
равен взаимной корреляционной функции сигналов
, то выходной сигнал будет
равен взаимной корреляционной функции сигналов ![]() и
и ![]() :
:
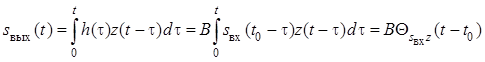 .
.
Таким образом, согласованный фильтр
вырабатывает на своем выходе взаимную корреляционную функцию, и, следовательно,
он может быть заменен коррелятором. В момент времени ![]() отношение
сигнал/шум на выходе согласованного фильтра будет равно отношению сигнал/шум на
выходе коррелятора с опорным сигналом, равным
отношение
сигнал/шум на выходе согласованного фильтра будет равно отношению сигнал/шум на
выходе коррелятора с опорным сигналом, равным ![]() .
Следует подчеркнуть, что при этом сигналы на выходе согласованного фильтра и
коррелятора не совпадают по форме.
.
Следует подчеркнуть, что при этом сигналы на выходе согласованного фильтра и
коррелятора не совпадают по форме.
К достоинствам согласованного фильтра можно отнести отсутствие генератора эталонного сигнала, который необходим для реализации коррелятора. Однако коррелятор считается более гибким устройством, так как для его перестройки достаточно заменить эталонный сигнал.
Пусть информационный сигнал ![]() является прямоугольным видеоимпульсом,
длительность которого равна
является прямоугольным видеоимпульсом,
длительность которого равна ![]() , а амплитуда –
, а амплитуда – ![]() :
:
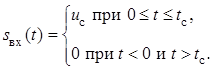
Примем задержку пика выходного сигнала
равной длительности входного сигнала: ![]() .
Поскольку сигнал является симметричным относительно
.
Поскольку сигнал является симметричным относительно ![]() , его импульсная
характеристика будет совпадать по форме с точностью до константы с
информационным сигналом:
, его импульсная
характеристика будет совпадать по форме с точностью до константы с
информационным сигналом:
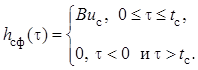
Структурная схема согласованного
фильтра с импульсной характеристикой приведена на рис. 3.1. Прежде всего
отметим, что реакцией идеального интегратора на дельта-импульс является единичный
скачок. Прямоугольный импульс с единичной амплитудой и длительностью ![]() представляет собой разность двух единичных
скачков, смещенных относительно друг друга на
представляет собой разность двух единичных
скачков, смещенных относительно друг друга на ![]() , откуда
следует, что фильтр, согласованный с прямоугольным видеоимпульсом, может
представлять собой каскадное соединение усилителя с коэффициентом усиления
, откуда
следует, что фильтр, согласованный с прямоугольным видеоимпульсом, может
представлять собой каскадное соединение усилителя с коэффициентом усиления ![]() , идеального интегратора и схемы вычитания
с идеальной линией задержки сигнала на
, идеального интегратора и схемы вычитания
с идеальной линией задержки сигнала на ![]() .
.
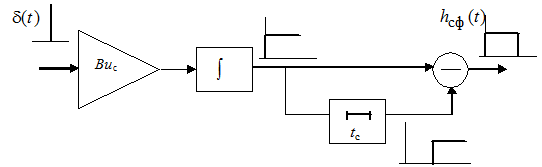
Рис. 3.1
Теперь построим этот же согласованный фильтр, используя спектральный метод. Спектральная плотность сигнала имеет вид
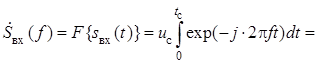
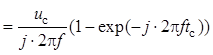 .
.
На основании выражения находим комплексную частотную характеристику согласованного фильтра
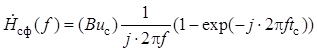 .
.
Поскольку идеальный интегратор имеет
комплексную частотную характеристику 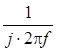 , а линия задержки –
, а линия задержки – ![]() , получим тот же результат, что и временным
методом.
, получим тот же результат, что и временным
методом.
Проведем анализ согласованного фильтра. Энергия входного сигнала с учетом равна
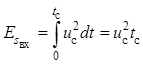 .
.
Тогда отношение сигнал/шум на выходе согласованного фильтра
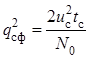 .
.
Подставив в и проведя несложные преобразования, найдем корреляционную функцию входного сигнала
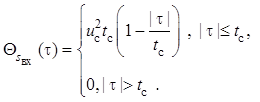
Подставив в и , получим, что сигнал и ковариационная функция шума на выходе фильтра, согласованного с прямоугольным видеоимпульсом, соответственно равны:

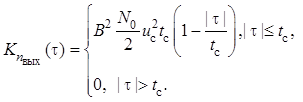
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.