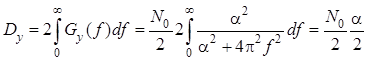Применение теории случайных процессов, страница 7

.

Применяя формулы , и , получим:

.

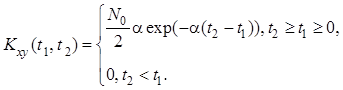
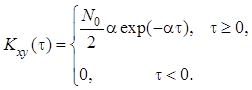
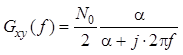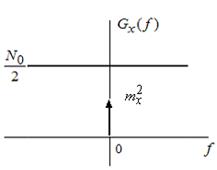
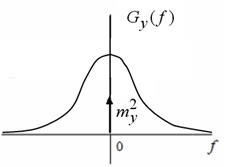
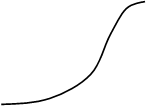
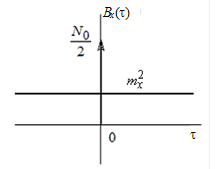
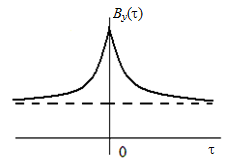
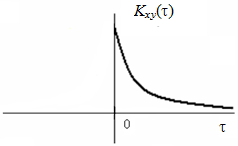
Корреляционные функции, спектральные плотности мощности и взаимная ковариационная функция входа и выхода схематически изображены на рис. 2.3. Напомним, что корреляционная функция вычисляется по формуле [5]

. ■

           

                    

Рис. 2.3

Пример 2.3. На высокодобротный параллельный колебательный контур, состоящий из параллельно соединенных резистора с сопротивлением , конденсатора с емкостью  и катушки с индуктивностью , воздействует ток , представляющий собой белый шум с нулевым математическим ожиданием и ковариационной функцией . Определить ковариационную функцию и дисперсию напряжения  на контуре в установившемся режиме.

Импульсная характеристика высокодобротного параллельного контура имеет вид (см. табл. 1.1)

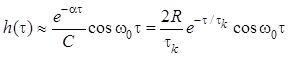, ,             где  – постоянная времени контура. Подставляя в , получаем:

.

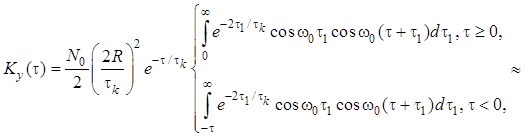
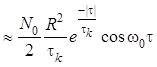В этом случае дисперсия выходного процесса будет

. ■                                   

2.5. Дифференцирование и интегрирование

случайных процессов

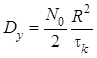Обычное определение производной нельзя применить к случайным процессам, так как отношение случайного процесса к приращению времени

является случайной величиной. Зафиксировав  и задав последовательность значений , сходящуюся к нулю, получим последовательность случайных величин. В этом случае можно говорить только о сходимости в вероятностном смысле.

Дадим определение сходимости последовательности случайных величин в вероятностном смысле. Последовательность случайных величин  называется сходящейся в среднеквадратическом к случайной величине , если существует предел

.

Случайную величину  называют пределом в среднеквадратическом смысле случайных величин  и пишут

.[1]

Говорят, что случайный процесс  дифференцируем, если существует такой случайный процесс , что

.

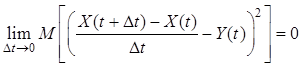В этом случае процесс  называют производной случайного процесса .

Итак, производная случайного процесса есть предел в среднеквадратическом отношения приращения случайного процесса  к приращению времени

.

Производная случайного процесса может также обозначаться традиционным образом:

.

Аналогично определяется интеграл от случайного процесса. Интегралом от случайного процесса  называют предел в среднеквадратическом соответствующей суммы

.

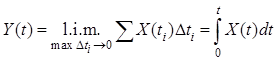Операции дифференцирования и интегрирования являются линейными. В теории вероятностей доказано, что они могут меняться местами с операцией математического ожидания, поэтому математическое ожидание производной стационарного случайного процесса

.               

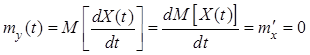Ковариационная функция производной случайного процесса

.

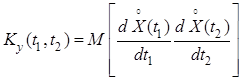Рассматривая  и  как независимые переменные, получим

.

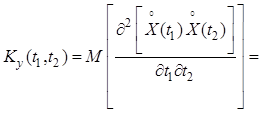
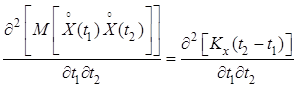Из соотношения  следует, что

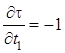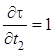 и , поэтому

.                       

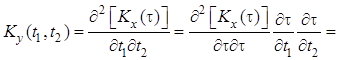
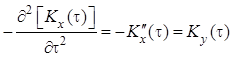Таким образом, ковариационная функция производной дифференцируемого случайного процесса равна второй производной его ковариационной функции, взятой со знаком минус

.                                  

Для дифференцируемости стационарного в широком смысле случайного процесса достаточно, чтобы его ковариационная функция была дважды дифференцируемой функцией.

Из формул и следует, что производная стационарного случайного процесса является стационарным случайным процессом, так как ее математическое ожидание равно нулю (т.е. не зависит от времени), а ковариационная функция зависит только от разности аргументов [5]. Так как дисперсия производной случайного процесса

, то условие дифференцируемости фактически равносильно условию конечности дисперсии .

Пример 2.4. Стационарный случайный процесс с экспоненциальной ковариационной функцией

                                    не является дифференцируемым, так как у ковариационной функции первая производная терпит разрыв в точке  и поэтому не существует ее второй производной. ■

Если случайный процесс , в свою очередь, дифференцируем, то его производная называется второй производной случайного процесса :

.

Аналогичным образом определяются производные более высоких порядков.

Пример 2.5. Стационарный случайный процесс с ковариационной функцией вида