Применение теории случайных процессов, страница 17

3.1.7. Согласованная фильтрация при небелом шуме

Пусть спектральная плотность мощности аддитивного шума , т.е.  является окрашенным шумом. Найдем характеристики согласованного фильтра для этого случая. При построении согласованного фильтра воспользуемся методом «выбеливающего» фильтра, который состоит в следующем. «Выбеливающий» линейный фильтр преобразует окрашенный шум  в белый шум  с равномерной спектральной плотностью мощности 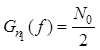. Реакцию «выбеливающего» фильтра на сигнал

можно представить в виде

, где  – оператор, определяющий свойства «выбеливающего» фильтра;  – информационный сигнал на выходе «выбеливающего» фильтра, который, естественно, отличается от , но может быть найден, если известна комплексная частотная характеристика этого фильтра. Тогда  представляет собой аддитивную смесь полностью известного сигнала  и белого шума . В этом случае фильтр, согласованный с  (максимизирующий отношение сигнал/шум ), по аналогии с имеет комплексную частотную характеристику

,                       где  и  – спектральная плотность и длительность сигнала .

Квадрат амплитудно-частотной характеристики «выбеливающего» фильтра должен удовлетворять условию

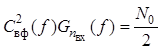, откуда

.

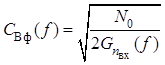Фазочастотная характеристика фильтра выбирается обычно из условия его физической осуществимости. Однако, как будет показано ниже, эта характеристика не влияет на комплексную частотную характеристику согласованного фильтра.

Спектральная плотность сигнала на выходе «выбеливающего» фильтра

.

Тогда комплексная частотная характеристика согласованного фильтра для сигнала на выходе «выбеливающего» фильтра с учетом будет

.

Согласованный фильтр для сигналов, наблюдаемых на фоне небелого шума, представляет собой последовательно соединенные «выбеливающий» фильтр и фильтр, согласованный c . В соответствии с комплексная частотная характеристика такого фильтра имеет вид

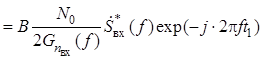, при этом отношение сигнал/шум

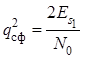, где

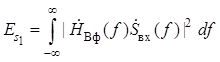
– энергия сигнала .

3.2. ФИЛЬТР ВИНЕРА

3.2.1. Синтез и анализ фильтра винера

Фильтрация информационных случайных процессов (называемых ниже сообщениями) из наблюдений, содержащих помехи, является обязательным элементом функционирования всех современных радиосистем – радиолокационных, связных, радионавигационных, радиоуправления и др. В математической постановке задача фильтрации выглядит следующим образом. На вход фильтра поступает наблюдаемый на бесконечном временном интервале сигнал

,                   содержащий сообщение  и помеху ,  – оператор, определяющий способ взаимодействия  и . Сообщение и помеха считаются стационарно связанными (необязательно гауссовскими) случайными процессами с нулевыми математическими ожиданиями. Ковариационная  и взаимная ковариационная  функции полагаются известными. Задача заключается в том, чтобы синтезировать линейный стационарный фильтр, формирующий оценку  случайного процесса , которая обеспечивает минимум среднеквадратической ошибки оценивания . Ясно, что успешно можно выделить сигнал из смеси сигнала и шума только в том случае, если свойства сигнала и шума резко различаются. В данном случае должны различаться спектрально-корреляционные характеристики сообщения и помехи.

В зависимости от объема входных данных, привлекаемых к образованию оценки , различают некаузальную и каузальную фильтрацию. Оценка и образующий ее фильтр называются некаузальными, если для получения  используются все входные данные . Если для получения  используются только прошлые данные, т.е. данные, уже поступившие к текущему моменту времени, то фильтр называется каузальным. Очевидно, что некаузальные фильтры не могут быть использованы в системах, формирующих оценку  в темпе поступления данных.

Выполним синтез некаузального стационарного линейного фильтра, использующего данные для оценки

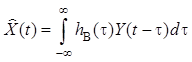                             и удовлетворяющего критерию минимума среднеквадратической ошибки оценивания . Пусть импульсная характеристика  минимизирует среднеквадратическую ошибку . Тогда произвольную импульсную характеристику линейной системы  можно представить в виде

, где  произвольная функция . При  величина среднеквадратической ошибки