Применение теории случайных процессов, страница 3

, где  – символ транспонирования комплексного числа.

Если линейная система состоит из двух последовательно соединенных линейных систем с характеристиками  и (или  и ), причем между двумя линейными системами отсутствует обратная связь, то импульсная характеристика  и комплексная частотная характеристика  этой системы имеют вид

,                 

.                              

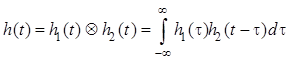Из следует, что амплитудно-частотная и фазочастотная характеристики составной системы определяются следующими соотношениями:

,

.

Задачи

1.  Определить, к какому виду относятся следующие операторы:

·  ,

·  ,

·  ,

·  ,

·  ,

·  ,

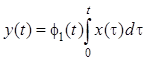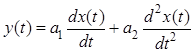·  , где  – вполне определенные неслучайные функции;  – заданные константы.

2.  Найти амплитудно-частотные и фазочастотные характеристики фильтров, приведенных на рис. 1.2 и 1.3.

                

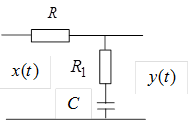
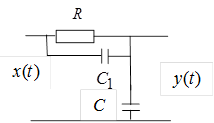
                       Рис. 1.2                                                          Рис. 1.3

3.  Найти амплитудно-частотные и импульсные характеристики фильтров, приведенных на рис. 1.4 и 1.5, где  – интегрирующий фильтр,  – высокодобротный параллельный колебательный контур,  – линия задержки.

            

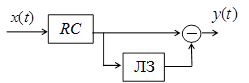
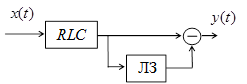
                      Рис. 1.4                                                                Рис.1.5

4.  Найти комплексную частотную характеристику интегратора со сбросом, связь между выходным и входным процессами которого задается следующим соотношением:

                            

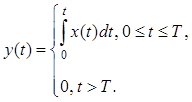
5.  Найти сигнал на выходе идеального интегратора, если на его входе действует видеоимпульс

                            

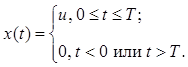
6.  Найти сигнал на выходе интегрирующей RC-цепи, если на ее входе действует видеоимпульс .

7.  Найти сигнал на выходе идеальной дифференцирующей цепи, если на ее входе действует видеоимпульс .

8. Найти сигнал на выходе дифференцирующей RC-цепи, если на ее входе действует видеоимпульс .

2. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМАХ

Одной из важнейших задач теории случайных процессов является задача определения вероятностных характеристик случайных процессов, полученных в результате преобразования некоторых других случайных процессов. В этом разделе рассмотрим преобразование стационарных в широком смысле случайных процессов [5] устойчивой стационарной линейной системой. Ограничимся рамками корреляционной теории, т.е. случаем, когда требуется определить только математическое ожидание и ковариационную функцию (или спектральную плотность мощности) выходного процесса, а также взаимную ковариационную (или взаимную спектральную плотность мощности) входного и выходного процессов [5].

Итак, на вход стационарной линейной системы  с комплексной частотной характеристикой  (или импульсной характеристикой ) воздействует стационарный в широком смысле случайный процесс  с известными математическим ожиданием  и ковариационной функцией . Реакцией линейной системы на входное воздействие  является случайный процесс

.

Необходимо найти математическое ожидание , ковариационную  и взаимную ковариационную  функции. Эта задача имеет достаточно простое решение, если линейный оператор  и операция математического ожидания  [5] могут меняться местами, т.е. когда

.                                   

В теории вероятностей доказано, что соотношение справедливо практически для всех линейных операторов.

2.1. Математическое ожидание

отклика линейной системы

Пусть на входе некаузальной линейной системы действует стационарный в широком смысле случайный процесс , тогда математическое ожидание процесса на ее выходе с учетом и будет равно

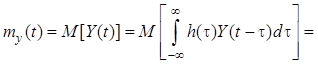
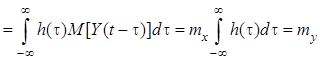, где интеграл  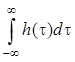равен значению комплексной частотной характеристики некаузальной линейной системы на нулевой частоте

.

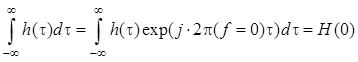Таким образом, математическое ожидание случайного процесса на выходе стационарной системы в установившемся режиме постоянно и равно произведению математического ожидания входного стационарного процесса на коэффициент передачи линейной системы по постоянной составляющей

.