Применение теории случайных процессов, страница 6

Взяв обратное преобразование Фурье от левой и правой частей формулы , получим формулу для вычисления ковариационной функции выходного процесса с помощью амплитудно-частотной характеристики линейной системы:

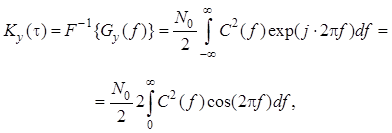
откуда следует, что дисперсия выходного процесса

.            

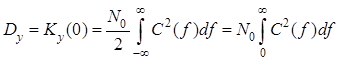Взаимную ковариационную функцию и взаимную спектральную плотность мощности процессов на входе и выходе линейной системы найдем, также используя фильтрующее свойство дельта-функции. В переходном режиме взаимная ковариационная функция для каузальной линейной системы

                   

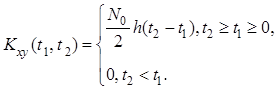
Подставив и в формулы , и , получим:

                           

,                                 

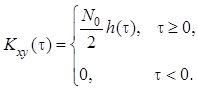
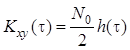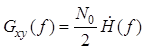,                                 где формула получена для каузальной системы, а – для некаузальной системы в установившемся режиме. Формула справедлива для обоих случаев.

Из и следует, что взаимная ковариационная функция для входного и выходного процессов стационарной линейной системы с точностью до постоянного множителя  равна импульсной характеристике этой системы. Очевидно, что для измерения импульсной характеристики линейной системы можно использовать взаимную ковариационную функцию. Схема такого измерителя приведена на рис. 2.2.

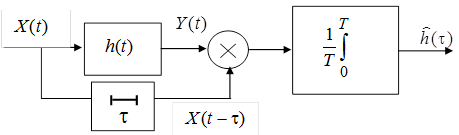
Рис. 2.2

Здесь полагается, что процессы  и  являются эргодическими [5] и взаимная ковариационная функция вычисляется путем усреднения по времени. Поскольку взаимная ковариационная функция  вычисляется с ошибкой, так как время интегрирования  является конечным, на рис. 2.2  обозначает, что импульсная характеристика  вычисляется приближенно. Точность вычисления  возрастает с увеличением . На практике вместо белого шума, мощность которого бесконечна, используется случайный процесс с равномерной спектральной плотностью мощности в полосе пропускания исследуемой линейной системы. Эффективная полоса входного воздействия должна быть тем шире, чем шире полоса пропускания линейной системы. Поскольку реальные линейные системы имеют ограниченную полосу пропускания, всегда можно подобрать случайный процесс с конечной мощностью. Достоинством такого метода вычисления импульсной характеристики является то, что мощность входного процесса может быть выбрана так, чтобы исследуемая система оставалась в линейном режиме при измерении импульсной характеристики.

Пример 2.2. Пусть на интегрирующую RC-цепь (рис. 2.1), начиная с момента , воздействует белый шум с математическим ожиданием  и ковариационной функцией . При  емкость разряжена. Найти спектрально-корреляционные характеристики выходного процесса.

Из следует, что квадрат амплитудно-частотной характеристики интегрирующей цепи равен

.                   

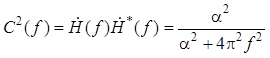Спектральная плотность мощности и корреляционная функция входного процесса имеют вид [5]:

,                            

.                              

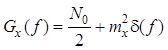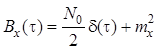Перемножив спектральную плотность мощности входного процесса и квадрат амплитудно-частотной характеристики интегрирующей цепи , получим

.                         

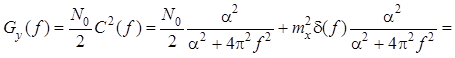
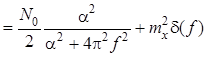Здесь учтено, что дельта-функция равна нулю на всех частотах, кроме , а амплитудно-частотная характеристика цепи на этой частоте равна единице. Для центрированного белого шума

.                            

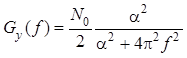Ковариационную функцию в установившемся режиме можно найти двумя способами. Взяв преобразование Фурье от левой и правой частей , получим

.

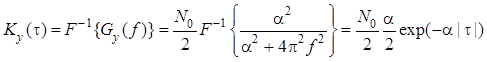Второй способ состоит в вычислении ковариационной функции по формуле . При  ковариационная функция выходного процесса равна:

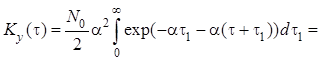
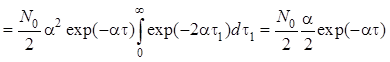,        а при  

.        

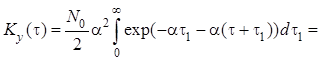
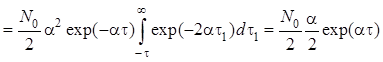Объединив и , получим

.                           

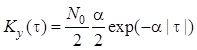Таким образом, при воздействии белого шума на RC-цепь выходной процесс имеет ковариационную функцию экспоненциального типа. Интервал корреляции этого процесса равен постоянной времени RC-цепи:

.

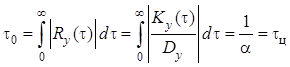Используя формулу , найдем ковариационную функцию выходного процесса для переходного режима:

   

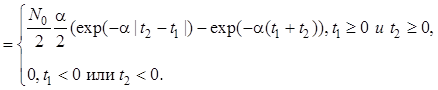
Теперь найдем дисперсию выходного процесса в переходном и установившемся режимах:

           

.                               

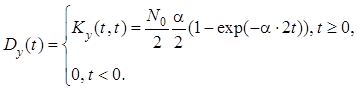
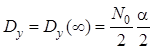Сравнивая и , нетрудно убедиться, что дисперсия  достигает уровня  в два раза быстрее, чем математическое ожидание. Формулу можно получить, используя :