Из следует, что согласованный фильтр превращает прямоугольный видеоимпульс в треугольный импульс удвоенной длительности. Ковариационная функция шума на выходе фильтра, согласованного с прямоугольным видеоимпульсом, также имеет треугольную форму. Интервал корреляции выходного шума
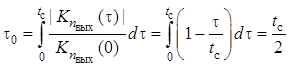 .
.
Структурная схема физически осуществимого фильтра, приведенная на рис. 3.1, содержит идеальные интегратор и линию задержки, поэтому практическая реализация такого фильтра возможна лишь в той мере, в какой характеристики реальных элементов можно приблизить к идеальным. В ряде случаев удается получить фильтры c существенно более простой реализацией, эффективность которых близка к оптимальному согласованному фильтру. Такие фильтры далее будем называть квазиоптимальными.
Для построения квазиоптимального
фильтра будем заранее задавать его структуру или комплексную частотную
характеристику с точностью до параметров. Далее будет выполняться
параметрическая оптимизация квазиоптимального фильтра в рамках заданной структуры.
Оптимальными будут считаться те значения параметров, при которых в
фиксированный момент времени отношение сигнал/шум на выходе квазиоптимального
фильтра достигает максимума. Очевидно, что отношение сигнал/шум на выходе
квазиоптимального фильтра не превысит ![]() .
Проигрыш в отношении сигнал/шум будет зависеть от того, насколько удачно была
выбрана его структура.
.
Проигрыш в отношении сигнал/шум будет зависеть от того, насколько удачно была
выбрана его структура.
Фильтр, согласованный с прямоугольным
видеоимпульсом, является фильтром нижних частот. Возьмем в качестве
квазиоптимального фильтра интегрирующую RC-цепь, которая является простейшим фильтром нижних
частот. Постоянную времени RC-цепи
![]() определим из условия максимума отношения
сигнал/шум
определим из условия максимума отношения
сигнал/шум
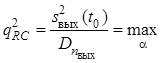 , где
, где ![]() и
и ![]() – сигнал в момент времени
– сигнал в момент времени ![]() и дисперсия шума
и дисперсия шума ![]() на
выходе RC-цепи.
на
выходе RC-цепи.
Сигнал на выходе интегрирующей RC-цепи при действии на ее входе прямоугольного видеоимпульса
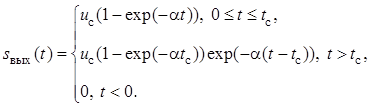
Из следует, что максимум полезного
сигнала на выходе интегрирующей RC-цепи достигается в момент окончания видеоимпульса, поэтому примем (так же
как и для согласованного фильтра) ![]() . В этом случае
максимальное значение выходного сигнала
. В этом случае
максимальное значение выходного сигнала
![]() .
.
Дисперсия шума на выходе RC-цепи при действии на ее входе белого шума в соответствии с
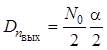 .
.
Подставив и в , получим
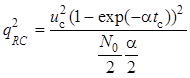 .
.
Выполнив элементарные преобразования, приведем выражение к виду
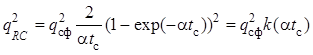 . где
. где ![]() –
отношение сигнал/шум для оптимального фильтра. График
зависимости
–
отношение сигнал/шум для оптимального фильтра. График
зависимости ![]() от
от ![]() приведен
на рис. 3.2, из которого следует, что
приведен
на рис. 3.2, из которого следует, что ![]() достигает
максимума, равного
достигает
максимума, равного ![]() , при
, при ![]() . Таким
образом, оптимальное значение постоянной времени интегрирующей RC-цепи:
. Таким
образом, оптимальное значение постоянной времени интегрирующей RC-цепи:
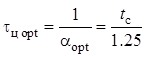 , при этом проигрыш в отношении
сигнал/шум оптимальному фильтру будет
, при этом проигрыш в отношении
сигнал/шум оптимальному фильтру будет
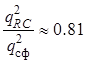 .
.
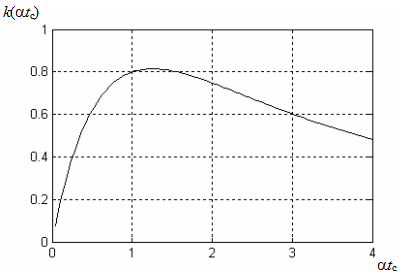
Рис. 3.2
Поэтому, чтобы отношение сигнал/шум на
выходе квазиоптимального фильтра было таким же, как и на выходе оптимального
фильтра, требуется энергию прямоугольного видеоимпульса увеличить примерно в ![]() раза.
раза.
В табл. 3.1 приведены эпюры сигналов и ковариационных функций для согласованного фильтра и интегрирующей RC-цепи.
Таблица 3.1
Характеристики фильтра и сигналов
|
Согласованный фильтр |
Интегрирующая RCцепь |
|
|
|
|
|
|
|
|
|
Окончание табл. 3.1
|
Согласованный фильтр |
Интегрирующая RCцепь |
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть информационный сигнал ![]() является прямоугольным радиоимпульсом c
амплитудой
является прямоугольным радиоимпульсом c
амплитудой ![]() , длительностью
, длительностью ![]() и
частотой
и
частотой ![]() :
:
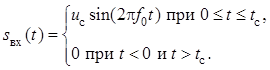
Для упрощения синтеза фильтра положим, что сигнал симметричен
относительно ![]() , т.е.
, т.е. ![]() . В
этом случае импульсная характеристика согласованного фильтра
. В
этом случае импульсная характеристика согласованного фильтра
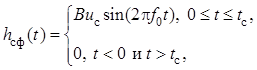
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.