Аналогичным образом определяется математическое ожидание случайного процесса на выходе каузальной стационарной линейной системы
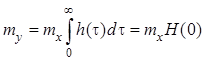 .
.
Если на каузальную линейную
систему воздействует случайный процесс ![]() ,
начиная с момента
,
начиная с момента ![]() , то математическое ожидание
случайного процесса на выходе линейной системы зависит от времени:
, то математическое ожидание
случайного процесса на выходе линейной системы зависит от времени:
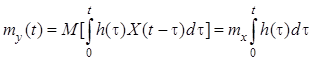 .
.
 В этом случае выходной процесс
В этом случае выходной процесс ![]() является
нестационарным, так как
является
нестационарным, так как ![]() – функция времени.
– функция времени.
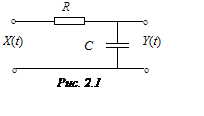
Пример 2.1. Пусть на интегрирующую RC-цепь (рис. 2.1), начиная с момента ![]() , воздействует случайный процесс
, воздействует случайный процесс ![]() с математическим ожиданием
с математическим ожиданием ![]() . При
. При ![]() емкость
разряжена. Найти математическое ожидание
емкость
разряжена. Найти математическое ожидание ![]() выходного
процесса
выходного
процесса ![]() .
.
Импульсная и комплексная частотная характеристики интегрирующей RC-цепи имеют вид (см. табл. 1.1):
![]() ,
,
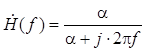 , где
, где ![]() ,
, ![]() – постоянная времени RC-цепи.
– постоянная времени RC-цепи.
Математическое ожидание
процесса ![]() в переходном режиме с учетом определяется следующей формулой:
в переходном режиме с учетом определяется следующей формулой:
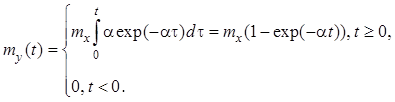
В установившемся режиме (при ![]() ) математическое ожидание
) математическое ожидание
![]() .
.
Это соотношение можно было получить,
используя формулу , так как на нулевой частоте
комплексная частотная характеристика равна единице ![]() .
.
Определим интервал времени ![]() , при котором переходной процесс можно
считать завершившимся, т.е. когда математическое ожидание выходного процесса
можно считать постоянным. Примем, что установившийся режим наступает, когда
, при котором переходной процесс можно
считать завершившимся, т.е. когда математическое ожидание выходного процесса
можно считать постоянным. Примем, что установившийся режим наступает, когда ![]() . Тогда из следует, что
. Тогда из следует, что
![]() .
.
Таким образом, интервал
времени ![]() прямо пропорционален постоянной времени RC-цепи. ■
прямо пропорционален постоянной времени RC-цепи. ■
Для определения
ковариационной функции отклика стационарной линейной системы найдем
центрированный случайный процесс ![]() . Для этого вычтем из
выражения выражение :
. Для этого вычтем из
выражения выражение :
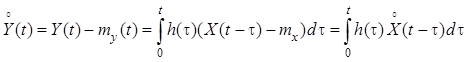 .
.
Далее запишем равенство для двух моментов времени ![]() и
и ![]() :
:
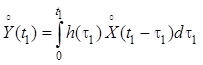 ,
,
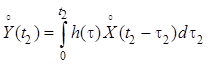 .
.
Взяв математическое ожидание от произведений левых и правых частей равенств и и затем поменяв местами операции взятия математического ожидания и интегрирования, получим
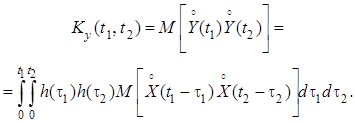
Отсюда следует, что ковариационная
функция отклика ![]() стационарной линейной каузальной
системы на воздействие
стационарной линейной каузальной
системы на воздействие ![]() , которое начинает действовать на
систему в момент времени
, которое начинает действовать на
систему в момент времени ![]() , равна:
, равна:
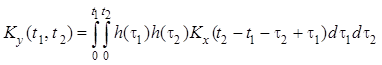 .
.
Приравняв ![]() к
к ![]() , получим выражение для дисперсии [5]
, получим выражение для дисперсии [5]
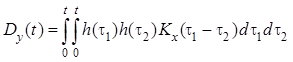 .
.
Из формул и [так же, как и из формулы ] следует, что выходной процесс ![]() нестационарен, хотя входной процесс
нестационарен, хотя входной процесс ![]() , воздействующий на линейную систему,
начиная с момента времени
, воздействующий на линейную систему,
начиная с момента времени ![]() , является стационарным
в широком смысле. Это объясняется тем, что система находится в переходном
режиме, который теоретически завершится при
, является стационарным
в широком смысле. Это объясняется тем, что система находится в переходном
режиме, который теоретически завершится при ![]() .
.
Найдем ковариационную
функцию и дисперсию случайного процесса ![]() на
выходе линейной системы, в которой завершился переходной процесс. Обозначив
на
выходе линейной системы, в которой завершился переходной процесс. Обозначив ![]() и перейдя к пределу
и перейдя к пределу ![]() в и , получим выражения для ковариационной
функции и дисперсии выходного процесса
в и , получим выражения для ковариационной
функции и дисперсии выходного процесса ![]() после завершения
переходного процесса в линейной системе:
после завершения
переходного процесса в линейной системе:
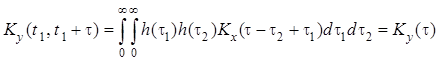 ,
,
 .
.
Отсюда следует, что процесс ![]() на выходе стационарной линейной системы
при стационарном входном воздействии является стационарным в широком смысле при
на выходе стационарной линейной системы
при стационарном входном воздействии является стационарным в широком смысле при
![]() , т.е. условия стационарности выходного
сигнала, строго говоря, предполагают его бесконечную длительность. На практике процесс
, т.е. условия стационарности выходного
сигнала, строго говоря, предполагают его бесконечную длительность. На практике процесс ![]() может
рассматриваться как стационарный после окончания переходных процессов в
линейной системе.
может
рассматриваться как стационарный после окончания переходных процессов в
линейной системе.
Для некаузальной линейной системы ковариационная функция и дисперсия выходного процесса:
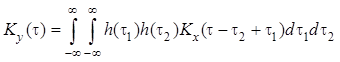 ,
,
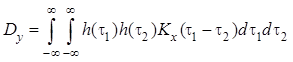 .
.
Взяв преобразование Фурье от левой и правой частей равенства , найдем спектральную плотность мощности стационарного в широком смысле случайного процесса на выходе стационарной линейной системы:
![]()
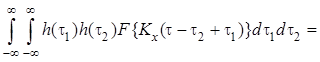
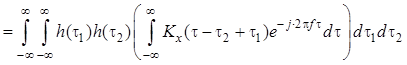 .
.
Заменив переменную под
знаком интеграла в круглых скобках ![]() и учитывая, что
импульсная характеристика и передаточная функция линейной системы связаны
преобразованием Фурье, получим
и учитывая, что
импульсная характеристика и передаточная функция линейной системы связаны
преобразованием Фурье, получим
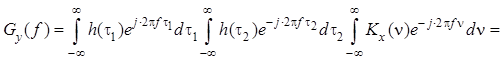
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.