Применение теории случайных процессов, страница 8

                                   дифференцируем неограниченное количество раз, так как существует неограниченное количество производных от этой функции. В частности, ковариационная функция и дисперсия первой производной равны:

,                        

.                                      

Дважды продифференцировав и умножив на , получим ковариационную функцию второй производной случайного процесса :

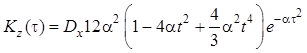, при этом дисперсия второй производной

. ■

Пример 2.6. Ковариационная функция случайного процесса :

.                           

Найти ковариационную функцию, дисперсию и интервал корреляции его производной.

Подставив в , получим

.       

Приравняв в  к нулю, найдем дисперсию производной случайного процесса  и ее нормированную корреляционную функцию [5]:

,

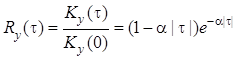, откуда интервал корреляции [5]

.

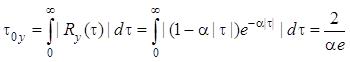Отметим, что интервал корреляции исходного процесса  равен

.

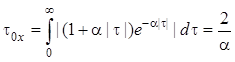Как и следовало ожидать, интервал корреляции  производной процесса меньше интервала корреляции  самого процесса, так как идеальный дифференциатор является фильтром верхних частот с комплексной частотной характеристикой  (см. табл. 1.1). При дифференцировании случайных процессов усиливаются верхние частоты и, как следствие, уменьшается интервал корреляции.

Нетрудно убедиться, что первая производная от терпит разрыв в точке , поэтому случайный процесс  с ковариационной функцией недифференцируем, а случайный процесс  с ковариационной функцией имеет только первую производную. ■

Теперь определим характеристики интеграла от стационарного случайного процесса. Очевидно, что математическое ожидание определяется следующим соотношением:

.        

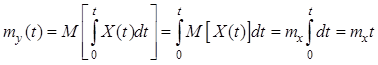Ковариационная функция интеграла от стационарного случайного процесса

.          

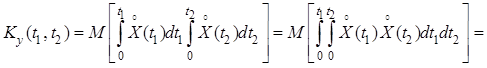
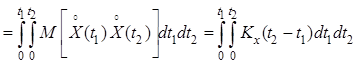Дисперсия интеграла от этого процесса зависит от времени и определяется формулой

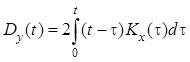,                            вывод которой дан, например, в [4].

Из формул и следует, что интеграл от стационарного случайного процесса является нестационарным случайным процес сом [5].

Пример 2.7. Найти ковариационную функцию интеграла от белого шума с ковариационной функцией

.                                  

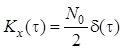По формуле найдем, что

.                      

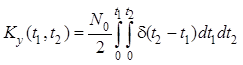При вычислении двукратного интеграла следует внимательно отнестись к тому, в каком порядке вычислять интегралы. Всплеск дельта-функции должен попасть в область интегрирования. Для этого необходимо интегрировать по переменной, имеющей больший диапазон. Пусть , тогда, интегрируя сначала по  и используя фильтрующее свойство дельта-функции, получим

.

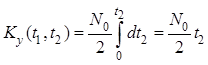Аналогично при , интегрируя сначала по , получим

.

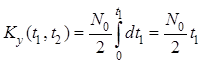Окончательное выражение для ковариационной функции имеет вид

.

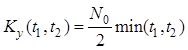Дисперсия процесса  

.                             

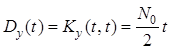Дисперсию процесса  также можно найти с помощью формулы . Подставив в , получим

.                   

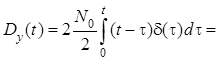
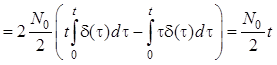При вычислении учтено, что

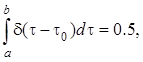
при или .

Таким образом, дисперсия интеграла от белого шума линейно возрастает с увеличением времени интегрирования . ■

Пример 2.7. Найти дисперсию интеграла от стационарного процесса , имеющего ковариационную функцию вида

.

В соответствии с формулой

. ■

2.6. Задачи

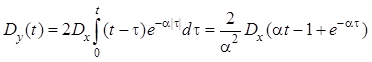1.  На вход фильтра, схема которого приведена на рис. 1.2, воздействует стационарный случайный процесс с корреляционной функцией 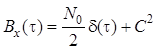. Найти спектральную плотность мощности и дисперсию выходного процесса.

2.  На вход фильтра, схема которого приведена на рис. 1.3, воздействует стационарный случайные процесс с корреляционной функцией 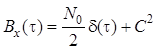. Найти спектральную плотность мощности и дисперсию выходного процесса.

3.  На вход идеального интегратора, начиная с , воздействует стационарный случайный процесс с корреляционной функцией . Математическое ожидание входного процесса больше нуля. Определить, через какое время математическое ожидание выходного случайного процесса достигнет величины .

4.  На вход идеального интегратора, начиная с , воздействует стационарный случайный процесс с корреляционной функцией . Определить дисперсию выходного процесса.

5.  На вход линейного фильтра с импульсной характеристикой