Применение теории случайных процессов, страница 13

Взяв обратное преобразование Фурье от , получим импульсную характеристику согласованного фильтра

.                                    

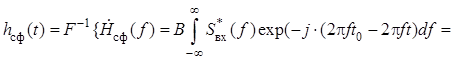
Таким образом, импульсная характеристика согласованного фильтра отличается от входного сигнала постоянным множителем , смещением во времени  и знаком аргумента . При замене знака перед аргументом  сигнал зеркально отображается относительно оси абсцисс, откуда следует: для того чтобы согласованный фильтр был физически осуществимым, необходимо, чтобы параметр  выбирался из условия , где  – длительность входного сигнала. Введение задержки не приводит к изменению отношения сигнал/шум, а лишь сдвигает по времени отклик фильтра. Обычно задержку  принимают равной длительности входного сигнала . Второе условие физической осуществимости согласованного фильтра состоит в том, что длительность сигнала  должна быть ограниченной. Если сигнал имеет неограниченную длительность, то задержка в согласованном фильтре должна быть бесконечно большой и согласованный с таким сигналом фильтр будет физически неосуществимым. На этом синтез физически осуществимого линейного фильтра, максимизирующего отношение сигнал/шум в момент времени , закончен. ■

Сделаем выводы по результатам синтеза.

1. Все спектральные составляющие сигнала на выходе согласованного фильтра в момент времени  имеют одну и ту же нулевую фазу, так как спектральная плотность выходного сигнала

,         откуда следует, что . Складываясь в фазе, спектральные составляющие выходного сигнала в момент времени  образуют пиковый выброс сигнала. Что касается шума, то, пройдя через фильтр с постоянными параметрами, он останется стационарным случайным процессом. При этом вероятность того, что стационарный шум на выходе согласованного фильтра в момент времени  образует выброс, очень мала.

2. Из следует, что фильтр, согласованный с сигналом , является оптимальным для всех сигналов той же формы, т.е. отличающихся от сигнала только амплитудой, так как значение константы  может быть произвольным.

3. Если сигнал является четной функцией относительно , то его импульсная характеристика с точностью до постоянного множителя равна входному сигналу.

3.1.3. Анализ согласованного фильтра

Проведем анализ согласованного фильтра. В первую очередь найдем отношение сигнал/шум на выходе согласованного фильтра в момент времени . Взяв обратное преобразование Фурье от , получим

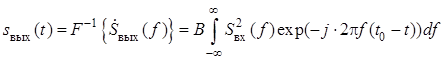, откуда сигнал на выходе в момент времени  будет

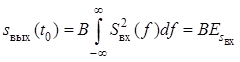, где

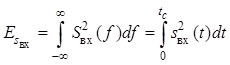
– энергия входного сигнала.

Таким образом, значение сигнала на выходе согласованного фильтра пропорционально энергии входного сигнала. Это обусловлено компенсацией фаз входного сигнала в согласованном фильтре.

С другой стороны, сигнал на выходе согласованного фильтра

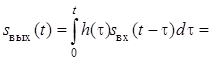
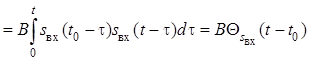,                где

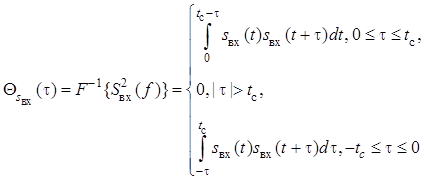
– корреляционная функция входного детерминированного сигнала. Из следует, что сигнал на выходе согласованного фильтра с точностью до постоянного множителя совпадает с корреляционной функцией входного детерминированного сигнала, сдвинутой вправо по оси времени на величину . Необходимо подчеркнуть, что корреляционная функция детерминированного сигнала  принципиально отличается от корреляционной функции случайного процесса. В частности, при  корреляционная функция детерминированного сигнала равна энергии этого сигнала, а корреляционная функция случайного процесса равна его полной мощности. При  сигнал на выходе согласованного фильтра

.

Рассмотрим теперь характеристики шума на выходе согласованного фильтра. При воздействии белого шума на вход согласованного фильтра спектральная плотность мощности шума на его выходе

.

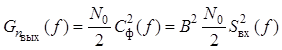Следовательно, ковариационная функция шума

                           .                 

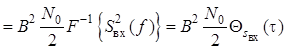Отсюда следует, что ковариационная функция шума на выходе согласованного фильтра с точностью до постоянного множителя 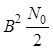 совпадает с корреляционной функцией входного сигнала. Шум на выходе согласованного фильтра коррелирован. Его интервал корреляции определяется корреляционной функцией входного сигнала. Из и следует, что ковариационная функция шума равна нулю при , т.е. отсчеты шума, взятые на расстоянии, превышающем длительность сигнала, являются некоррелированными. Таким образом, можно считать, что интервал корреляции шума на выходе согласованного фильтра равен .