Порог чувствительности измерительной системы. Чувствительность к форме сигнала. Пределы измерений, динамический диапазон

на), является нелинейным, нельзя говорить о чувствительности, так как отношение выходного сигнала у ко входному сигналу x: меняется в зависимости от величины х. Для таких нелинейных систем мы введем дифференциальную чувствительность. По определению, дифференциальная чувствительность S_diff измерительной системы, описываемой соотношением у = f(x), при входном сигнале х₀ равна

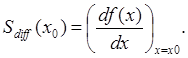
В случае линейной системы S_diff ≠ S_diff (x₀) и S_diff = S . У нелинейной системы S_diff зависит от значения входного сигнала х.

Возьмем, например, нуль-детектор с передаточной функцией у = ах — Ьх³, где а > О и b > 0. Дифференциальная чувствительность такого устройства уменьшается с ростом входного сигнала. Для нуль-детектора особенно важно, чтобы дифференциальная чувствительность была высокой при очень малых входных сигналах. Чем больше S_diff (0), тем лучше можно обнаружить выполнение нулевого условия и тем более точным может быть измерение.

Другой мерой чувствительности нелинейной системы служит коэффициент чувствительности. Для измерительной системы с сигналом х на входе и сигналом у на выходе (с передаточным соотношением у = f(x)) коэффициент чувствительностиопределяется как

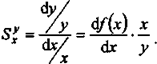Само обозначение указывает на то, что данный множитель характеризует чувствительность у к изменениям в х В случае линейной системы Sx является плохой мерой чувствительности, так как Sx = 1 , какой бы ни была величина S.

Мы уже имели дело с коэффициентами чувствительности при обсуждении вопроса о распространении ошибок измерения (раздел 2.3.2). Другим примером использования коэффициента чувствительности в метрологии является тензодатчик. В этом датчике происходит преобразование изменения длины Δl в изменение сопротивления ΔR Коэффициент чувствительности тензодатчика Sl равен

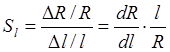Отметим, что введенная выше чувствительность системы S является безразмерной только в том случае, когда у и х имеют одинаковую размерность. Это никогда не выполняется, например, в случае датчиков. У дифференциальной чувствительности S_diffта же размерность, что и у чувствительности S. Однако, коэффициент чувствительности всегда безразмерен.

Порог чувствительности

Невозможно увеличивать чувствительность измерительной системы до бесконечности (например, путем увеличения коэффициента усиления): идя по этому пути, мы столкнемся с порогом чувствительности.

Порог чувствительности измерительной системы определяется как наименьший входной сигнал, который все еще обнаруживается с заданной вероятностью правильного решения. Порог чувствительности препятствует обнаружению нами сколь угодно малых сигналов. Это обусловлено тем, что во всякой реализуемой физической системе имеются спонтанные, случайные флуктуации (шум), из-за которых малый по величине измеряемый входной сигнал «тонет» в этом (образующем фон) шуме. Шум в измерительной системе может быть обусловлен многими причинами, такими как тепловые колебания (шум резистора) или квантовый характер потока зарядов, масс или носителей энергии через потенциальный барьер (дробовой шум электронов, ионов или фотонов).

Помимо принципиально неизбежных флуктуационных шумов в измерительной системе существуют и другие источники возмущений, которые могут затемнять полезный сигнал. Например, механические вибрации или электрические наводки могут давать настолько большой сигнал на выходе, что слабые сигналы, действующие на входе, уже нельзя обнаружить. Такие механические дефекты как трение, люфт или наличие мертвой зоны могут приводить к тому, что входной сигнал ниже определенного порога чувствительности не будет приводить к появлению сигнала на выходе. Часто простым изменением конструкции измерительной системы эти нефундаментальные ограничения можно устранить.

Принципиальный предел чувствительности системы определяется случайными флуктуациями внутри этой системы и является существенной характеристикой. В измерительной системе всегда присутствует шум, и он определяет теоретически осуществимый порог чувствительности.

Мы рассмотрим вопрос о пороге чувствительности шумящей измерительной системы в предположении, что измеряемая величина х остается постоянной. Пусть шум имеет гауссово распределение. Тогда при х = 0 выходной сигнал будет обладать плотностью распределения f_n(x) су = 0 (см. рис. 2.28). Если ко входу приложен сигнал х ≠ 0, то выходной сигнал будет складываться из желаемого сигнала у и (того же самого) шума. Плотность распределения в этом случае обозначим f_sn(y).

Теперь перед нами стоит важный вопрос: какой величины сигнал х можно обнаружить? Другими словами, при каком значении y мы все еще можем отличить наблюдаемую ситуацию от случая, соответствующего x = о и, следовательно, у = 0 ?Ответ на этот вопрос зависит от степени определенности, с какой мы хотим знать, спрятан в шуме полезный сигнал или его нет. В постановке задачи нетрудно разобраться, следуя приводимым ниже рассуждениям. Предположим, что среднеквадратическое значение шума на выходе σ (стандартное отклонение распределения f_n(y)) равно n-й части выходного сигнала у . В силу того, что плотность распределения вероятностей