Динамический сигнал можно анализировать как во временной области, так и в частотной области. Наблюдение структуры колебания, например, с помощью осциллографа, осуществляется во временной области, тогда как частотное наполнение (свойства) изучают с помощью спектроанализатора в частотной области.
Следовательно, для однозначного определения того, что такое «чувствительность измерительной системы» в случае динамического сигнала необходимо установить, на какую характеристику сигнала реагирует наша измерительная система. Другими словами: значение какого параметра сигнала измеряется! Применительно к динамическому измерительному сигналу x(t) можно указать следующие характерные значения:
- Пиковое значение хр:
хр= max|x(t)|.
- Полный размах хрp:
хрр = max {x(t)} - min {x(t)}.
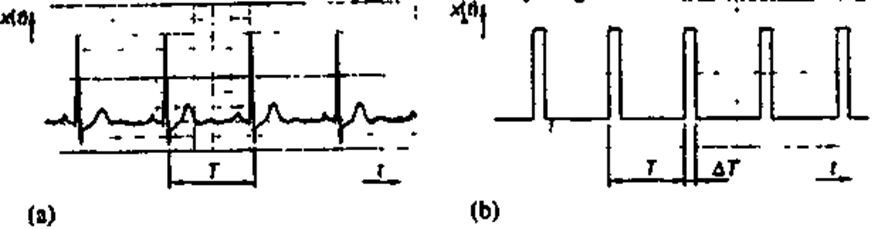
Рис 2 29 Периодические сигналы (а) Сложный периодический сигнал общего вида (Ь) Импульсный сигнал с коэффициентом заполнения ΔT/T = 1/7
Целесообразно как можно реже использовать пиковое значение и полный размах, так как оба они очень чувствительны к возмущениям типа шума, накладывающегося на полезный сигнал. Большие ошибки в xp и xppвозникают также из-за нелинейных искажений сигнала. Значительно менее чувствительными к искажениям и помехам являются следующие параметры сигнала:
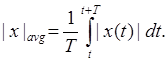 |
Среднее значение периодического сигнала находят на интервале времени, в который укладывается целое число периодов: Т = п/f, п — целое. Среднее значение синусоидального сигнала равно нулю.
Среднее значение от абсолютной величины |x|avg
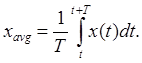
Когда говорят о среднем значении синусоидального сигнала, обычно имеют в виду среднее значение абсолютной величины синусоидального колебания. - Действующее значение xRMS
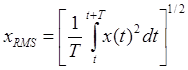
Сейчас будет показано, что применение действующего значения в качестве характеристики измерительного сигнала полезно. Мгновенная мощность p(t), рассеиваемая на резисторе R приложенным к нему измерительным сигналом x(t), равна
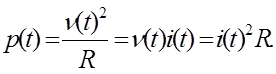
Здесь i(t) — ток, текущий по резистору R Средняя мощность, рассеиваемая на резисторе за время Т, равна
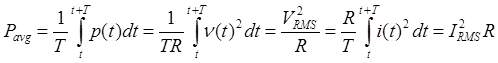
Cледовательно, воспользовавшись действующими значениями напряжения и тока, мы легко можем найти (среднее) значение мощности, рассеиваемой измерительным сигналом. Очевидно, что можно также принять, по определению, что среднеквадратические значения напряжения и тока —
это такие величины постоянного напряжения и постоянного тока, при которых в резисторе переходит в тепло такое же количество энергии, какое рассеивается в нем при воздействии измеряемых напряжения или тока (тепловое определение действующего значения).
При построении измерительной системы решают вопрос о том, на какое характерное значение сигнала будет реагировать система. Измерительная система может воспроизводить мгновенные значения сигнала (осциллограф), откликаться на среднее значение (измеритель с подвижной катушкой), реагировать на среднее значение от абсолютной величины (измеритель с подвижной катушкой, снабженный выпрямителем/усилителем) или быть чувствительной к среднеквадратическому значению (электродинамический вольтметр).
Для синусоидального сигнала x(t) = asin(wt), изображенного на рис. 2.30, значения перечисленных параметров равны:
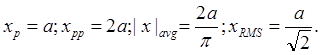
Отношение xRMS/|x|avg называют коэффициентом формы сигнала x(t), а отношение хp/xkms — коэффициентом амплитуды этого сигнала (его пик-фактором). Для синусоидального колебания коэффициент формы равен 1,11, а пик-фактор — √2 . Коэффициент формы важен в том случае, когда измерительная система проградуирована в действующих значениях (для синусоидального колебания), а фактически ею измеряется среднее значение от абсолютной величины. Именно так обстоит дело во многих электронных вольтметрах. Пик-фактор важен при измерениях шумовых и импульсных сигналов. Часто бывает желательно знать действующее значение таких сигналов, однако при этом необходимо, чтобы пиковые значения сигналов оставались в линейном диапазоне системы; только в этом случае мы избежим ошибок измерения, обусловленных насыщением.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.