Если сумма двух синусоидальных колебаний разных частот подана на вход нелинейной системы, то выходной сигнал будет содержать гармоники. Гармониками являются синусоидальные колебания с частотами nw1 и kw2 соответственно, где n и k — целые числа. При п, k = 1 мы имеем дело с основными гармониками, а большим значениям n и k соответствуют высшие гармоники n-го и k-го порядков. Кроме того, в выходном сигнале появятся также составляющие с суммарными и разностными частотами пw1± kw2, где w1 > w2 и n>k. Помимо этого выходной сигнал может иметь также постоянную составляющую.
Раскладывая соотношение у =f(x) для статической нелинейной системы в ряд Тейлора, например, в точке х = 0, легко видеть, что
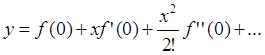
Полагая
f(0)=0, f'(0) = с1, f''(0)=c2
и т. д.
И
x(t)=x1(t)+x2(t), где x1(t) = a1 sinw1(t)
и x2(t) = a2 sinw2(t) , получим:
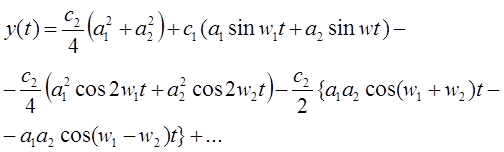
Степень нелинейности измерительной системы характеризуется нелинейными или гармоническими искажениями. Искажение такого рода измеряется путем подачи на вход измерительной системы одиночного синусоидального колебания. Коэффициент искажения, по определению, равен отношению действующего значения уп n-й гармоники к действующему значению у1основной (первой) гармоники. Таким образом, коэффициент искажения, обусловленного n-й гармоникой, определяется как
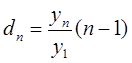
Полный коэффициент искажений, обусловленных п — 1 гармониками (за исключением основной гармоники n = 1)), равен
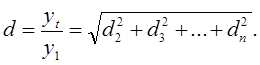
Это соотношение легко понять, приняв во внимание, что корень из суммы квадратов действующих значений гармоник представляет собой действующее значение всех п — 1 гармоник:
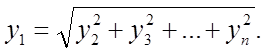
Степень статической (частотно-независимой) нелинейности часто определяют по-другому. Предположим, что в действительности соотношение между у и х задается функцией у =f(x), как показано на рис. 2.31. Лучшим линейным приближением кривой у =f(x) является прямая у = ах. В этом случае мерой нелинейности измерительной системы может служить максимальное значение выражения
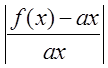
в пределах всего динамического диапазона измерительной системы. Об определенной таким образом нелинейности говорят также, как о нелинейности с нулевым смещением.
Никакая измерительная система не является идеально линейной; она всегда линейна лишь приближенно (например, в малом интервале значений входного сигнала х). Сейчас мы кратко рассмотрим несколько видов нелинейности, которые могут иметь место в практических измерительных системах. Прежде всего речь пойдет о некоторых видах статической нелинейности.
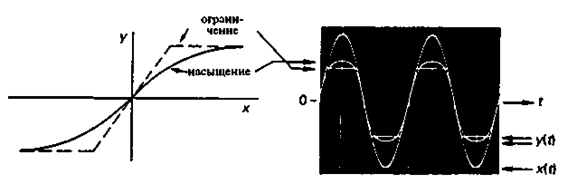
Насыщение и ограничение. Нелинейность такого рода характеризуется уменьшением дифференциальной чувствительности Sdiff с ростом входного сигнала х. Как показано на рис. 2.32, в случае ограничения такое ослабление наступает резко, а в случае насыщения — постепенно. Чтобы предотвратить выход измерительной системы из строя, когда она оказывается перегруженной
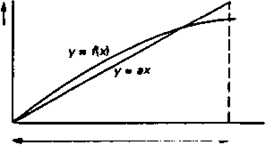
Рис. 2.31. Статическая нелинейность.
(a) (b)
Рис. 2.32. Примеры насыщения и ограничения в измерительной системе, (а) Нелинейные передаточные характеристики. (Ь) Сигнал y(t), возникающий на выходе системы под действием синусоидального входного сигнала X(t).
ной слишком большим входным сигналом, часто намеренно ограничивают размах выходного сигнала безопасными значениями.
— Гистерезис. Такая нелинейность вызывается различными кривыми на плоскости ху, выражающими связь между у и х при увеличении х и при уменьшении х (см. рис. 2.33). К гистерезису может привести, например, люфт в механической зубчатой передаче. Другой пример гистерезиса — это зависимость магнитной индукции В от напряженности поля H у ферромагнитного материала (кривая намагничивания).
— Мертвая зона. Этот вид нелинейности обычно возникает в том случае, когда существуют одна или большее число областей, в пределах которых величина выходного сигнала у не зависит от входного сигнала х (см. рис. 2.34). Такая нелинейность может быть вызвана трением покоя. Объект (например, стрелка) не будет двигаться до тех пор, пока действующая сила не превысит трения покоя.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.