Динамическое поведение линейной измерительной системы также целиком определено, если известно, как она реагирует на синусоидальное колебание меняющейся частоты; то есть в том случае, когда мы знаем частотную характеристику.
Определение частотной характеристики измерительной системы приводит нас к (комплексной) зависимости чувствительности от частоты s(co). Чувствительность системы S(w) состоит из двух характеристик: из амплитудно-частотной характеристики |S(w)| и фазо-частотной характеристики АгgS(w). Этими двумя зависимостями динамическое поведение линейной системы определяется полностью. Характеристикой частотных свойств служит ширина полосы f0. Значение f0 представляет собой частоту, на которой мощность выходного сигнала падает вдвое по сравнению с максимальной мощностью на выходе. Следовательно, на частоте f0 амплитуда выходного сигнала уменьшается в √2 раз по сравнению с ее значением на низких частотах. Поэтому значение амплитудно-частотной характеристики на частоте f0 равно S(0)/√2 при условии, что на постоянном токе соответствующая величина равна S(0). Графики, приведенные на рис. 2.37, служат иллюстрацией сказанного. Так как 20log10(1/√2)≈-3 , частоту f0 называют также частотой спада на 3 дБ (сокращенно: точкой «-3 дБ»). Белы и децибелы служат логарифмической мерой отношения мощностей. Эта мера рассмотрена в приложении A3.
Рис. 2.36. Отклик y(t) линейной измерительной системы на входное воздействие х(t) в форме скачка. Переходная характеристика нормализована таким образом, что у'(t) = y(t) / S(0), где S(0) — чувствительность системы по постоянному току. Время установления прибора при допустимой погрешности ±Dy0 / y0 равно ts.
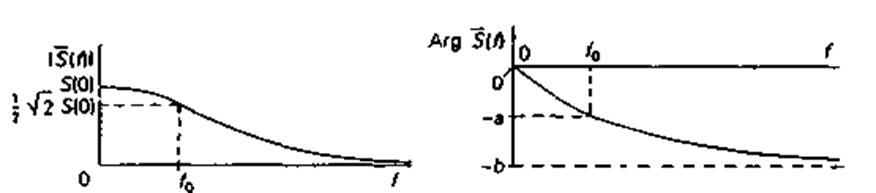
Рис. 2 37 Частотная характеристика S(f), состоящая из двух зависимостей: амплитудно-частотной характеристики | S(f)| и фазо-частотной характеристики Arg S(f )Ширина полосы системы равна f0.
Соотношение между входной величиной x(t) и выходной величиной y(t), а значит, и динамическое поведение линейной динамической системы можно представить в виде линейного дифференциального уравнения.
Если у зависит от х, то дифференциальное уравнение, описывающее соотношение между у и х, содержит не только функции от у и от х, но также и производные по времени от этих функций. В линейном дифференциальном уравнении имеются только такие члены, в которые функция у и ее производные входят в первой степени. Порядок дифференциального урав-нения равен наивысшему из порядков входящих в него производных
У многих измерительных систем, различных по своей природе (электрических, тепловых, акустических и т. д.), динамическое поведение оказывается сходным. Если описывать эти системы в обобщенном виде в терминах V- и I-величин, то мы будем получать одни и те же дифференциальные уравнения. Следовательно, при изучении динамических систем можно ограничиться только дифференциальными уравнениями определенного вида. С точки зрения динамического поведения особенно важным является порядок дифференциального уравнения. С учетом этого говорят об (измерительной) системе п-го порядка и об отклике n-го порядка, если поведение системы можно описать с помощью дифференциального уравнения n-го порядка. На практике большинство измерительных систем можно с достаточной точностью описать линейным дифференциальным уравнением второго или более низкого порядка. Поэтому наше рассмотрение будет включать только случаи, когда п принимает одно из трех значений: О, 1 или 2.
Дифференциальное уравнение, описывающее систему нулевого порядка, является лишь простым алгебраическим уравнением. Система является статической или, говоря другими словами, частотно-независимой. Примером системы нулевого порядка служит потенциометрический преобразователь смещения, изображенный на рис. 2.38(а). В этом датчике смещение х преобразуется в пропорциональное ему выходное напряжение V. Предположим, что сопротивление между нижним концом потенциометра и движком равно
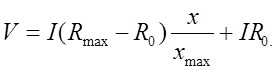 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.