Порог чувствительности измерительной системы. Чувствительность к форме сигнала. Пределы измерений, динамический диапазон, страница 11

Или

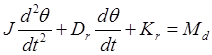
В результате, как и следовало ожидать, мы пришли к линейному дифференциальному уравнению второго порядка.

Чтобы сделать более ясной аналогию с другими системами, указанными на рис. 2.42, перепишем полученное уравнение, введя новую переменную w = dq /dt:

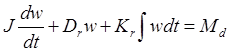
Отклоняющий момент M_d является I-величиной (см приложение А 4), а угловая скорость w — V-величиной. Вращающаяся механическая система аналогична системе с поступательным движением, изображенной на рис 2.42(b). Эта последняя состоит из груза массы т, пружины с коэффициентом упругости K_t и демпфера с постоянной затухания D_t Если на систему действует сила F_d то скорость v груза по отношению к земле удовлетворяет равенству

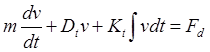
Поскольку v=dx/dt , мы снова приходим к тому же самому линейному дифференциальному уравнению второго порядка, что и полученное ранее. Наконец, обе механические системы — с вращательным и с поступательным движениями — аналогичны электрической системе, показанной на рис. 2.42(с). На этот параллельный электрический контур действует I-величина: по нему течет ток I_d Мы хотим определить V-величину, являющуюся решением уравнения:

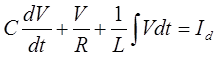
Это уравнение эквивалентно обоим уравнениям, полученным выше Все различие может состоять в том, что I-величины и V-величины поменяются местами. Структура системы остается одной и той же, когда мы переходим от J к т или С, одновременно заменяя D_r на D_t или 1 / R, а также К_r - на К_t,или 1 / L (см. приложение А. 4). Принимая во внимание, что

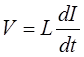
последнее уравнение можно переписать в виде:

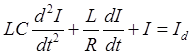
где I представляет собой ток, текущий по катушке L

Мы видим теперь, что дифференциальное уравнение, описывающее линейную систему второго порядка, в общем случае содержит  две постоянные а  и b:

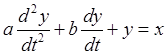
Здесь х — это величина входного воздействия х(t), а у — выходная величина у(t), нормализованная по отношению к чувствительности по постоянному току S(0), так что  у=y(t)./S(0). Благодаря нормализации третья постоянная в дифференциальном уравнении отсутствует. Чтобы сделать запись более наглядной, введем две другие постоянные: относительное затухание z и угловую частоту w₀ свободных незатухающих колебаний в системе, и перепишем общее уравнение с использованием этих констант:

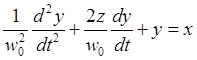
В случае системы с вращением переменные и параметры, входящие в это уравнение, имеют вид:

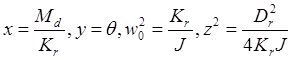
а в случае системы с поступательным движением —

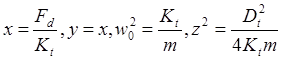Для электрической цепи имеем

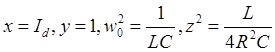Соответствующее уравнение в операторной форме выглядит так:

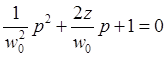И корни его равны

Необходимо различать следующие три характерных случая   z < 1, z  = 1 и z > 1.

Недостаточное демпфирование (z <  1)

Можно показать, что отклик системы y(t) на входной сигнал, имеющий форму скачка величины x₀, происходящего в момент t = 0, равен

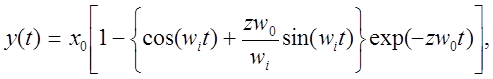
где ;при выводе этого выражения предполагается, что начальные значения у(0) и (dy/dt)_t=o равны нулю. Конечное значение, достигаемое в установившемся режиме, равно

.

Непосредственно вслед за входным скачком возникают затухающие ко лебания с частотой w_i, наложенные на конечное значение (см рис. 2 43) Мы видим, что с ростом z затухание колебаний происходит все быстрее Поэтому z называют относительной скоростью затухания.Если z = 0, то колебания в системе продолжаются и их частота равна w₀; система находится в режиме свободных колебаний.Таким образом, w₀ — это резонансная частота системы, в которой затухание отсутствует полностью

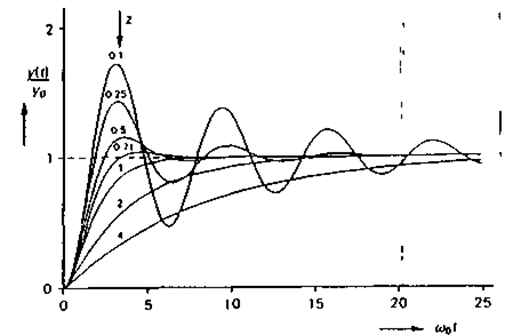
Рис.2.43. Переходные характеристики системы второго порядка при различных значениях относительного коэффициента z.

Критическое демпфирование (z = 1)

Предполагая снова, что начальные условия являются нулевыми, то есть у(0) = 0 и (dy/dt)_t=o = 0, а величина скачка на входе в момент t = 0 равна х₀, получаем следующее выражение для переходной характеристики системы второго порядка при z=1:

Как и ранее, конечное значение у₀равно х₀, но теперь на выходе нет затухающих колебаний (см. рис 2 43).