(a) (b)
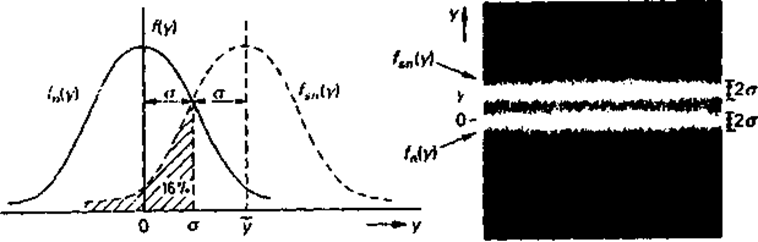
Рис.2.28. Порог чувствительности измерительной системы, подверженной действию шума, (а) Плотность распределения вероятностей для сигнала на выходе системы в отсутствие сигнала на входе (fn(у)) я при его наличии (fsn(y)). (b) Выходной сигнал как функция времени в случае, когда сигнала на входе нет (х = 0), и в случае, когда на входе действует сигнал, вызывающий появление на выходе постоянного напряжения у .
fn(y) является четной функцией, мы можем ввести критерий обнаружения, основанный на том, что фактическое значение выходного сигнала у больше или меньше, чем 0,5 у. Представим себе, что у- это выборочное значение выходного сигнала. Тогда нам необходимо иметь возможность сделать вывод о наличии сигнала у на основе единственной выборки у. (Когда мы можем позволить себе отложить принятие решения и взять среднее от нескольких выборок, это фактически означает осуществление низкочастотной фильтрации. В этом случае вероятность обнаружения значительно возрастает, так как увеличивается эффективное отношение сигнал/шум.) Если у > 0,5у, то мы делаем вывод, что сигнал на входе присутствует, а если у < 0,5 у, то мы принимаем решение об отсутствии сигнала на входе. На рис. 2.28(b) показан случай, когда берется большое число выборок, как при наличии входного сигнала, так и в его отсутствие. Здесь п примерно равно 3 (у = Зσ). При n=2 темная полоска между двумя изображениями выходного шума на экране осциллографа исчезает. В последнем случае мы уже не можем четко различать эти два изображения; на рис. 2.28(а) показаны соответствующие плотности распределения. Что значит надежность обнаружения в этом случае? Как можно видеть из графика на рис. 2.28(а), приу = 2σ (п = 2) (согласно критерию обнаружения, при котором происходит сравнение со значением 0,5 у) заключение, что «входного сигнала нет», будет ошибочным для 16% выборок. Это в точности та часть всей площади под fsn(y), которая заштрихована. Поэтому доля случаев, в которых обнаруживается входной сигнал, порождающий выходной сигнал у = 2 , составляет 84%. Следовательно, с достоверностью 84% можно обнаруживать маскируемое шумом постоянное напряжение, когда среднеквадратическое значение шума равно половине значения этого постоянного напряжения (п =2). Отношение сигнал/шум в данном случае составляет (пσ)2/σ2 = п2 = 4 Это рассуждение показывает, что желаемая степень надежности определяет порог чувствительности (значение п).
В табл. 2.3 приведена достоверность или вероятность обнаружения сигнала на входе по критерию y > 0,5 y , вычисленная для нескольких значений у .
Табл. 2.3. Вероятность обнаружения и отношение сигнал/шум для различных значений сигнала у в зависимости от соотношения между стандартным отклонением σ и величиной сигнала.
|
Сигнал у |
Вероятность обнаружения |
Отношение сигнал/шум |
|
1 σ |
69,15% |
1 |
|
1,4 σ |
76,11% |
2 |
|
2 σ |
84,13% |
4 |
|
3 σ |
93,32% |
9 |
|
4 σ |
97,72% |
16 |
|
5 σ |
99,38% |
25 |
|
6 σ |
99,87% |
36 |
|
8 σ |
99,9968% |
64 |
|
10 σ |
99,999971% |
100 |
Общепринятой мерой порога чувствительности является величина входного сигнала, для которого отношение сигнал/шум равно единице. Тогда, в случае шума с нормальным распределением мгновенных значений, вероятность обнаружения оказывается равной примерно 70%.
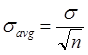 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.